Напряженность как градиент потенциала

Сила Кулона 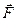, действующая со стороны электростатического поля на пробный точечный заряд 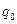, и потенциальная энергия 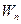этого заряда равны

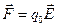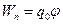, . (10.25)

С другой стороны, между потенциальной силой 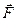и потенциальной энергией 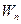существует, как и при рассмотрении гравитационного поля в механике, связь

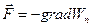. (10.26)

Подставив сюда формулы (10.25) и сократив на заряд 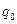, получим:

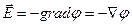, (10.27)

где дифференциальный оператор Гамильтона 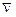(набла)

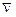
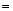
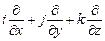. (10.28)

Из (10.27) следует, что проекции вектора 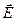на оси декартовой системы координат связаны с частными производными от потенциала 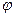по этим координатам:

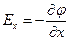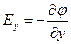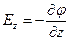, , . (10.29)

Элементарная работа сил электростатического поля по перемещению пробного заряда 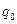на расстояние 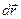равна

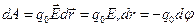, или ,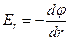

где - проекция вектора напряженности 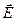на направление радиуса вектора .

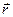Для полей с центральной или осевой симметрией соотношение (10.27) можно преобразовать к виду

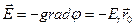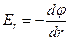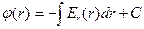, , , (10.30)

где 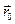- единичный вектор, коллинеарный с вектором 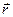, 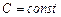– постоянная интегрирования.

Используя соотношения (10.27) - (10.30), можно получить формулы:

- для расчета потенциала электростатического поля точечного заряда и заряженного шара радиуса 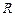на расстоянии ( ≥ )

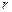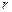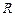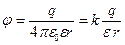, (10.31)

- для расчета потенциала электростатического поля тонкой прямой бесконечной заряженной нити с линейной плотностью 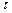или цилиндра радиуса 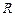на расстоянии ( ≥ )

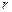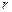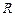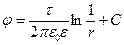, (10.32)

где 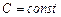– постоянная интегрирования.

В различных задачах электростатики используется понятие объемной 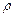, поверхностной 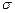и линейной 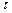плотности заряда

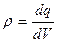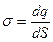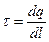, , . (10.33)