Электростатического поля
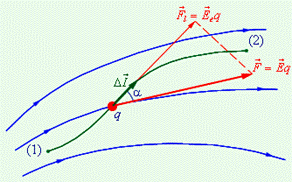
При перемещении пробного заряда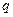 
в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении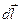 
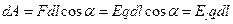, (10.18)
где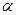 
- угол между вектором напряженности 
и вектором перемещения , 
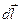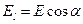- проекция вектора нанаправление перемещения .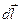
Электростатическое поле обладает важным свойством:
Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.
Аналогичным свойством обладает и гравитационное поле, и в этом нет ничего удивительного, так какгравитационные и кулоновские силы описываются дуальными (подобными) соотношениями.
|
| Рис. 10.11 |
Следствием независимости работы от формы траектории является следующее утверждение:
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.
Силовые поля, обладающие этим свойством, называют потенциальными или консервативными.
Докажем потенциальность электростатического поля на примере поля точечного заряда. Вычислим работу сил электростатического поля точечного заряда 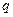при перемещении пробного заряда 
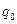по произвольной траектории от точки 1 с радиусом 
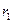до точки 2 с радиусом 
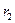(рис. 10.12). Подставив в соотношение (10.18) напряженность 
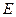поля точечного заряда (10.6) и проинтегрировав (10.18) от 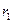до 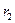, получим:
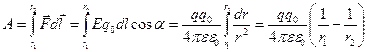. (10.19)
Здесь учтено, что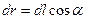 
.
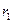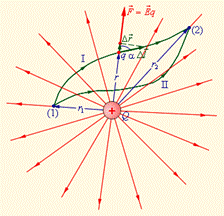
Видно, что работа сил поля не зависит от формы траектории, а зависит только от начальной и конечной 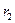точек траектории. На траекториях I и II, изображенных на рис. 10.12, работы кулоновских сил одинаковы. Если на одной из траекторий изменить направление перемещения заряда 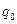на противоположное, то работа изменит знак. Отсюда следует, что на замкнутой траектории работа кулоновских сил при перемещении произвольного заряда равна нулю, т.е. рассмотренное поле является потенциальным.
Свойство потенциальности электростатического поля может быть записано через циркуляцию вектора напряженности электростатического поля вдоль произвольного замкнутого контура 
:
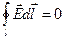. (10.20)
Свойство потенциальности электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. Для этого в пространстве выбирается некоторая точка, например, бесконечность ( 
), где потенциальная энергия заряда 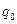, помещенного в эту точку, принимается равной нулю.
|
| Рис. 10.12 |
Потенциальная энергия заряда 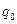, помещенного в произвольную точку поля 1, равна работе 
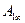, которую совершит электрическое поле при перемещении заряда 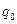из точки 1 в бесконечность ( ).
Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора точки ( ), где энергия равна нулю. Такая неоднозначность в определении потенциальной энергии не приводит к каким-либо недоразумениям, так как физический смысл имеет не сама потенциальная энергия, а разность ее значений в двух точках пространства.
Работа, совершаемая электрическим полем при перемещении точечного заряда 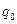из точки 1 в точку 2, равна разности потенциальных энергии в этих точках и не зависит от формы пути перемещения заряда.
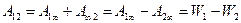. (10.21)
Потенциальная энергия заряда 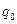, помещенного в электрическое поле, пропорциональна величине этого заряда.
Физическую величину, равную отношению потенциальной энергии электрического заряда 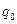в электростатическом поле к величине этого заряда 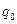, называютпотенциалом 
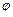электрического поля:
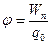. (10.22)
Потенциал 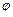является энергетической характеристикой электростатического поля. Он равен работе сил поля при удалении положительного единичного заряда из данной точки поля в бесконечность. Потенциал является скалярной величиной и, как и напряженность , подчиняется принципу суперпозиции.
Разность потенциалов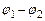 
между двумя точками 1 и 2 равна работе электростатического поля при переносе единичного заряда между этими точками и называется напряжением 
:
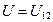. (10.23)
Таким образом, работа 
по перемещению электрического заряда 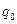из точки 1 в точку 2 равна произведению заряда 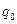на разность потенциалов :
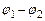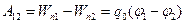. (10.24)
Для наглядного представления электрического поля наряду с силовыми линиями вектора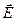 
используют эквипотенциальные поверхности величины 
.
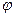Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.
Силовые линии 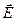электрического поля всегда перпендикулярны эквипотенциальным поверхностям.
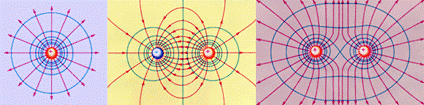
Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рис. 10.13 представлены картины силовых линий и эквипотенциальных поверхностей точечного заряда, электрического диполя и двух равных положительных зарядов.
|
| Рис. 10.13 |
Дата добавления: 2015-08-04; просмотров: 1407;