Локальный (дифференциальный) признак потенциальности электростатического поля.

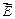Найдем циркуляцию вектора по бесконечно малому плоскому прямоугольному контуру 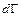, расположенному в районе некоторой точки, в декартовой системе координат. Нас будет интересовать конфигурация (линейные размеры) этого контура, поэтому изобразим его достаточно большим. Выберем направление обхода по контуру – против часовой стрелки.

Т.к. величины dx и dy являются очень маленькими, можно считать, что и поле на протяжении этих отрезков также одинаково; будем обозначать поле в каждой точке стороны 1 как , поле в каждой точке стороны 2 как 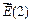, и так далее. Интеграл по замкнутому контуру в данном случае мы можем заменить на сумму четырех слагаемых:

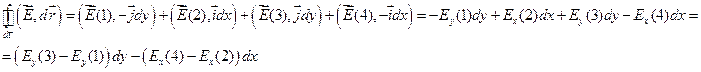
Теперь заметим, что выражение по сути является приращением y-ковой составляющей поля при переходе из 1 в 3 вдоль оси x. Тогда наше выражение приблизительно равно:

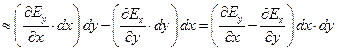
Мы нашли циркуляцию вектора 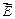по элементарному контуру.

Аналогично для элементарных прямоугольных контуров в плоскостях yz и zx можно получить:

А так как циркуляция вектора 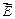по любому контуру равна нулю, то можно сделать вывод, что в потенциальном поле выполняются одновременно все 3 следующих равенства:

(*)

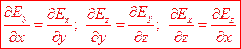То, что выписано – необходимый, а в электростатике – и достаточный признак потенциальности электрического поля в декартовой системе координат.

Выполнение этих равенств проверить на практике гораздо проще, чем проверять интегральный признак потенциальности электростатического поля.

Итак, поле 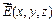является потенциальным в области, если условия (*) выполняются в каждой точке этой области.

Условия (*) можно компактно записать в векторной форме, если ввести в рассмотрение вектор "ротор" напряженности электрического поля (см. Замечание).

Замечание

Ротор вектора 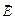определим следующим образом

Векторное произведение вектора оператора градиента и вектора напряженности электрического поля, или ротор 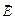можно записать через детерминант

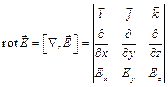
Следовательно, для электростатического поля имеем