Нормировка потенциала или выбор уровня отсчета.

Перепишем формулу (3) иначе:

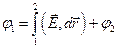- определен с точностью до выбора некой постоянной 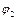, которая нам не известна.

Существуют два удобных способа выбора значения аддитивной постоянной.

1. Если система зарядов занимает ограниченную область пространства, то потенциал бесконечно удаленной точки обычно полагают равным нулю. Потенциал любой другой точки согласно однозначно определится выражением

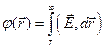
2. В практике электрических измерений часто полагают равным нулю потенциал поверхности Земли. При этом исходят из того, что вследствие очень большой электрической емкости Земли ее потенциал практически неизменен и соединение какого-либо проводника с Землей (заземление) делает его потенциал практически фиксированным. В этом случае

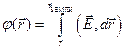
Когда говорят о потенциале, то имеют ввиду разность потенциалов 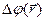между рассматриваемой точкой и точкой, потенциал 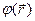которой принят за 0.

Вообще, физический смысл имеет величина, которая может быть измерена. Поэтому говорят, что потенциал 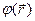в данной точке физического смысла не имеет, так как нельзя измерить работу в данной точке. Физический же смысл имеет разность потенциалов.

Потенциал характеризуется аддитивностью и он подчиняется принципу суперпозиции, как и вектор напряженности электрического поля.

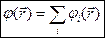
Если электрическое поле создано системой точечных зарядов, то потенциал 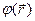в данной точке равен алгебраической сумме потенциалов 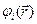, созданных в этой точке каждым из зарядов в отдельности.

С использованием разности потенциалов квазистатическая работа сил поля при перемещении заряда q₀ по произвольному пути из точки 1 в точку 2 представится на основании (3) как

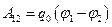(4)

т.е. квазистатическая работа сил поля равна убыли потенциала, умноженной на величину перемещаемого заряда.

Единицей измерения потенциала служит вольт (В). Если между двумя точками пространства для переноса заряда в один кулон требуется совершить работу в один джоуль, то разность потенциалов в этих точках равна одному вольту.

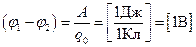
2.6. Локальное (дифференциальное) соотношение между 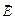и .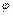

Рассмотрим 2 близкие точки 1 и 2 на координатной оси OX в электростатическом поле 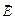. В соответствии с определением приращения потенциала, поскольку точки очень близки, а значит и потенциалы близки:

.

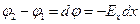Получается, что .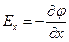

Если точки 1 и 2 лежат в произвольной точке пространства, то аналогичное соотношение можно получить для проекции напряженности на другие оси декартовой системы координат:

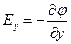
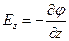
Таким образом, вектор 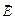может быть представлен в виде:

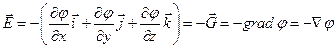
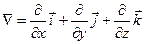- это оператор Гамильтона (1805-186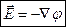5).

(5)

(читается так: «Набла фи»).

2.7. Физический смысл градиента (подробно прочитать- литература [6], стр.80-82)

Рассмотрим приращение потенциала d 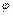вдоль произвольно ориентированного элемента перемещения 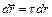. Величина d 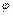зависит, с одной стороны, от распределения поля 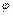(x, y, z) в пространстве, а с другой стороны, от выбора точек сравнения 2 и 1. Учитывая малость dr, можно записать

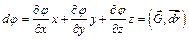(6)

Здесь

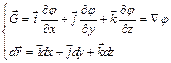
Рассмотрим величину d 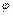при перемещении точки 2 по элементарной сфере радиусом dr (вектор 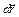меняется только по правлению) (рис.1.). Из формулы (6), записанной в виде

,

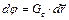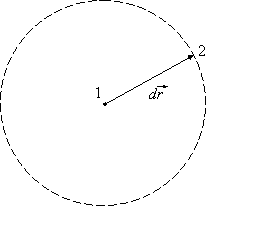
Рис.1. Элементарный вектор 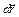c закрепленным в точке 1 началом. При изменении положения 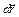в пространстве точка 2 движется по поверхности сферы

видно, что максимальная величина 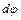соответствует такому направлению 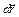, при котором 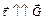(так как 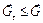), другими словами:

1) направление вектора градиента потенциала указывает направление наиболее быстрого возрастания поля 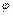в пространстве;

2) величина вектора 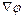определяет “скорость” пространственного изменения поля 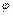в направлении его наиболее быстрого возрастания (Возможно, следовало выразиться как-то осторожней, чтобы не связывать понятие скорости, имеющее смысл производной по времени, с величиной производной по координате, однако такое словоупотребление весьма распространено в литературе);

3) “скорость” пространственного изменения потенциала в произвольном направлении (задаваемом вектором 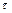) равна проекции вектора градиента на это направление.

На основании изложенного выше и выражения (5) приходим к следующему утверждению.

Вектор поля 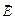в данной точке пространства направлен в сторону наиболее резкого уменьшения потенциала, а его величина равна скорости убыли потенциала в этом направлении.

Введем понятие эквипотенциальной поверхности - поверхности, во всех точках которой потенциал имеет одно и то же значение.

Выделим поверхность одинакового потенциала и построим в любой ее точке локальную систему координат ХYZ так, что оси ОХ и ОY будут касательны к эквипотенциальной поверхности, а ось OZ направим по нормали к поверхности в сторону возрастания потенциала (рис. 2).

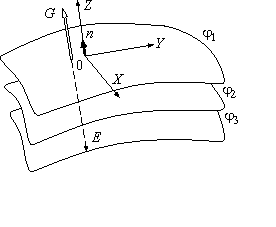
Рис. 2. Взаимное расположение трех эквипотенциальных поверхностей ( 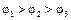), вектора 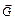градиента потенциала и вектора 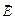напряженности электрического поля. Изображена также локальная декартова прямоугольная система координат XYZ, ось Z которой направлена вдоль нормали 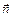к элементу поверхности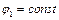

По построению 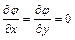в точке 0 и, следовательно,

,

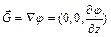т.е. вектор градиента поля, а значит, и вектор 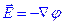, нормален к эквипотенциальной поверхности в любой ее точке. Поскольку направление 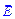определяет направление силовых линий, то очевиден вывод о том, что линии поля нормальны к эквипотенциальным поверхностям.

Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.

Силовые линии электростатического поля всегда перпендикулярны эквипотенциальным поверхностям.

Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы.

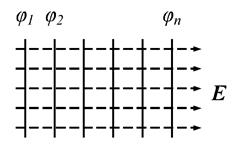
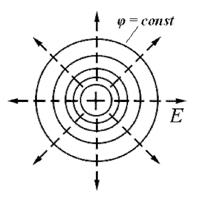Для однородного поля эквипотенциальные поверхности параллельные линии.

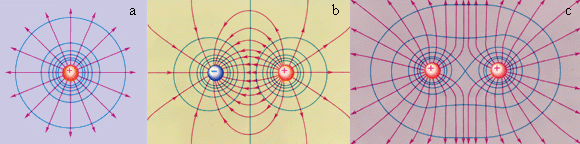
На рис. представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.

Рисунок Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полей: a – точечный заряд; b – электрический диполь; c – два равных положительных заряда