Интегральный признак потенциальности электростатического поля.

Анализируя полученную формулу для работы сил электростатического поля по перемещению заряда q по некоторому контуру Г, можно сделать следующие выводы:

1) работа 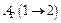не зависит от формы контура Г, а зависит только от начального и конечного положений;

2) если точки 1 и 2 совпадают (контур Г – замкнутый), то 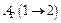=0, т.е.

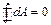
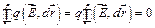
Линейный интеграл, взятый по замкнутому контуру (замкнутой кривой) Г, называется циркуляцией вектора 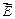. Т.е. утверждается, что циркуляция электростатического поля равна нулю.(Теорема о циркуляции).

Последний результат справедлив и для электростатического поля, созданного любой системой покоящихся точечных зарядов, т.к. по принципу суперпозиции электростатических полей

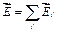
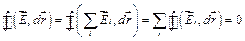
Векторное поле называется потенциальным, если циркуляция этого вектора по любому замкнутому контуру 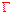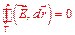равна нулю.

Однако этот критерий потенциальности является неудобным на практике, т.к. нужно будет исследовать всевозможные контуры (что само по себе невозможно), и установить, является ли интеграл по ним равным нулю.