Градиент потенциала

Градиент потенциала – это скорость возрастания потенциала в направлении кротчайшем между двумя точками.

Между двумя точками имеется некоторая разность потенциалов. Если эту разность разделить на кратчайшее расстояние между взятыми точками, то полученное значение будет характеризовать скорость изменения потенциала в направлении кратчайшего расстояния между точками.

Градиент потенциала показывает направление наибольшего возрастания потенциала, численно равен модулю напряженности и отрицательно направлен по отношению к нему.

В определении градиента существенны два положения:

1) Направление, в котором берутся две близлежащие точки, должно быть таким, чтобы скорость изменения была максимальной.

2) Направление таково, что скалярная функция в этом направлении возрастает.

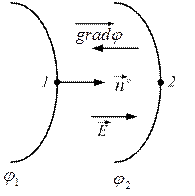
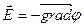
Для декартовой системы координат:

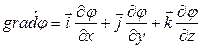
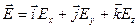
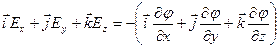
Скорость изменения потенциала в направлении оси Х, Y, Z:

; ;

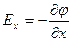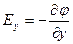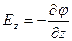
Два вектора равны только тогда, когда равны друг другу их проекции. Проекция вектора напряженности на ось Х равна проекции скорости изменения потенциала вдоль оси Х, взятой с обратным знаком. Аналогично для осей Y и Z.

; ; .

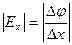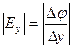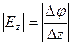В цилиндрической системе координат выражение градиента потенциала будет иметь следующий вид:

.

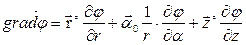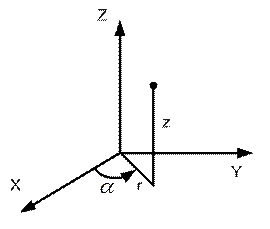
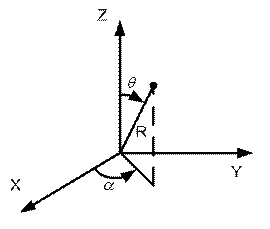
А в сферической системе координат:

.

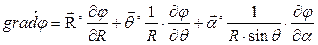Дифференциальный оператор Гамильтона (оператор Набла)

Для сокращения записи операций над скалярными и векторными величинами употребляют дифференциальный оператор Гамильтона или оператор Набла:

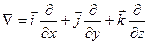
Под дифференциальным оператором Гамильтона понимают сумму частных производных по 3-м координатным осям, умноженных на соответствующие единичные векторы (орты).

Применим оператор Гамильтона к потенциалу:

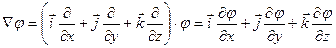
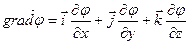
Правые части одинаковы, значит, будут одинаковы и левые части:

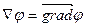
Оператор Гамильтона сочетает в себе как векторные, так и скалярные свойства и может быть применен к скалярным и векторным функциям.