Свойства дискретных передаточных функций

Передаточную функцию ЛИС запишем, используя матрицы системы разностных уравнений описывающих динамические свойства объекта:

,

,

,

,

.

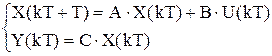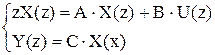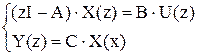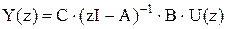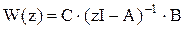Отметим очень важное свойство передаточной функции ЛИС: прядок полинома её числителя у большинства объектов равен (n-1), за исключением систем с запаздыванием и систем, у которых степени полинома числителя и знаменателя непрерывной передаточной функции совпадают.

Представим эту передаточную функцию для одноканального объекта в виде отношения полиномов:

.

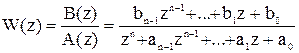Коэффициент усиления статического объекта может быть найден как:

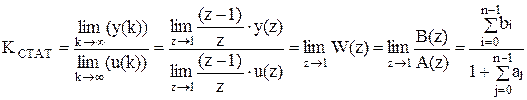
От передаточной функции можно перейти к разностному уравнению

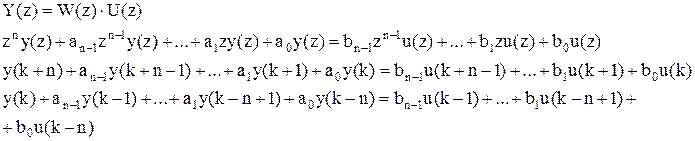
Последнее равенство получено из предыдущего путем сдвига аргумента. Как видим, текущее значение y(k) зависит от «n» предыдущих значений y(i) и u(i), в этом и состоит свойство памяти динамических систем.