Одномерные моментные функции СП.
Математическое ожидание случайного процесса 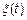 определяется в следующем виде
определяется в следующем виде
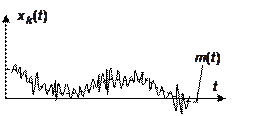
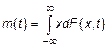
Определение МО: Математическое ожидание – это среднее, вокруг которого изменяются мгновенные значения СП.
Замечание!!!: Усреднение производится по всем реализациям.
В случае, когда математическое ожидание постоянно, т.е. 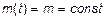 его называют постоянной составляющей СП
его называют постоянной составляющей СП 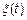 . МО изменяющееся во времени носит название тренда СП.
. МО изменяющееся во времени носит название тренда СП.
Центрированным процессом или флуктуациями называется СП вида
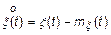
Для СП вводятся начальные и центральные моментные функции, которые определяются соответственно
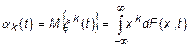 ,
,
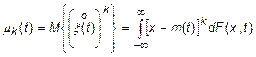 ,
,
где 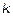 - порядок моментной функции.
- порядок моментной функции.
Запишем центральный момент второго порядка, который представляет собой дисперсию СП 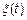
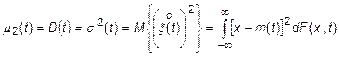 .
.
где  – среднеквадратическое отклонение, определяемое как
– среднеквадратическое отклонение, определяемое как 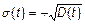 .
.
В свою очередь начальный момент первого порядка представляет собой математическое ожидание СП 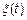 .
.
Дисперсия СП и его математическое ожидание выражаются друг через друга при помощи начального момента второго порядка, т.е.
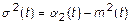
Начальные и центральные моменты связаны взаимнооднозначно через характеристическую функцию 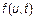
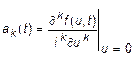 ,
, 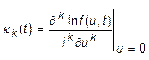 – кумулянты.
– кумулянты.
 – математическое ожидание,
– математическое ожидание,
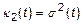 – дисперсия.
– дисперсия.
Кумулянтные коэффициенты определяются следующим образом
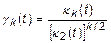 .
.
Дата добавления: 2015-08-04; просмотров: 999;
