Отметим основные свойства ФР

1. Не убывает по каждому аргументу .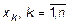

2. Непрерывна слева по каждому аргументу .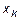

3. Свойство нормированности заключается в том, что выполняются следующие условия:

a. , при всех .

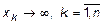b. 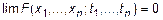, если хотя бы один из аргументов .

4. Свойство симметрии

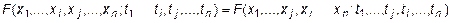
Другими словами, функция распределения не изменится, переставляя местами аргументы мы переставим и соответствующие этим аргументам параметры.

В общем случае это свойство можно переписать в следующем виде

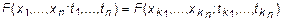
5. Функция распределения безразмерная функция.

Два СП называются независимыми, если их совместная ФР равна произведению ФР каждой из них

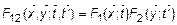
В зависимости от свойств непрерывности 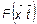мгновенные значения СП могут быть:

- Непрерывными;

- Дискретными;

- Смешанными.