Зонные пластинки. Фокусировка

Открывая постепенно диафрагму, можно наблюдать в точке P рост результирующего колебания. Этот рост закончится, когда диафрагма целиком откроет первую зону Френеля (E₁).

При дальнейшем увеличении диафрагмы начнут открываться области второй зоны. Результирующая амплитуда в точке наблюдения начнёт уменьшаться. Она станет почти нулевой, когда окажутся открытыми первые две зоны Френеля.

Затем вновь начнётся рост амплитуды: открывается третья зона. Открытие четвёртой зоны ознаменуется снижением амплитуды. Таким образом, каждая чётная зона «гасит» волну от предыдущей нечётной.

На рисунке 7.12 приведена векторная диаграмма для случая, когда чётные зоны отсутствуют. Как это можно сделать? Для этого надо изготовить такую преграду-маску, которая закрывала бы все чётные зоны но оставалась бы прозрачной для нечётных (Пример такой маски – на рис. 7.13).

Рис. 7.12

Рис. 7.13

Амплитуда колебаний в точке P в этом случае резко возрастёт (рис. 7.12). Это результат того, что удалось исключить гасящее влияние чётных зон.

Можно создать преграду, прозрачную для всех зон, но такой формы, чтобы оптический ход волны от каждой чётной зоны оказался бы на λ больше оптического хода волны от предыдущей нечётной зоны (рис. 7.14).

Рис. 7.14

a в

Рис. 7.15

В этом случае чётные зоны не исключаются. Их фаза увеличивается на π, и они создают в точке наблюдения колебания, синфазные с колебаниями соседних нечётных зон.

Соответствующая векторная диаграмма представлена на рис. 7.15а.

Ну и, наконец, можно ведь создать зонную пластинку более тонкой структуры. Пластинку, влияющую не на целые зоны, а только на подзоны. Это означает, что следует ступенчатую зонную пластинку заменить собирающей линзой. Эффект ее действия представлен на векторной диаграмме 7.15в.

Итог лекции 7.

1. Принцип Гюйгенса - Френеля. Интеграл Френеля:

.

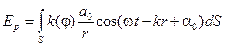Лекция 8 «Дифракция волн»

(Продолжение)

План лекции

1. Дифракция Фраунгофера от длинной щели

2. Интенсивность дифракционной картины

3. Критерий типа дифракции

Итог лекции 8

На прошлой лекции обсуждался принцип Гюйгенса-Френеля. Был записан интеграл Френеля:

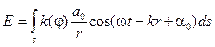(8.1)

В качестве иллюстрации, поясняющей Принцип, была рассмотрена дифракция Френеля от круглого отверстия. Напомним, что дифракция Френеля — это дифракция в «сходящихся - расходящихся» пучках.

Теперь обратимся к дифракции в параллельных пучках – к дифракции Фраунгофера.