Дифракция Фраунгофера от длинной щели

Пусть волна от бесконечно удалённого источника падает на непрозрачный экран, в котором прорезано прямоугольное отверстие.

Это отверстие называют длинной прямой щелью, если длина отверстия (l) значительно превышает его ширину (b): 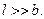За щелью поместим собирающую линзу, а в её фокальной плоскости — экран наблюдения (рис. 8.1).

Рис. .8.1

Таким образом будет выполнено условие дифракции Фраунгофера.

Разделим поверхность щели на узкие полоски dx, параллельные боковым краям щели. Возникшие элементарные зоны являются источниками вторичных волн. Так как линза собирает плоские волны, то их амплитуды не будут зависеть от расстояния до экрана r.

Кроме того, ограничившись малыми углами дифракции φ, можно считать

k (φ) = 1.

Эти соображения позволяют упростить подынтегральное выражение в формуле Френеля (8.1). Амплитуду волны, приходящей от элемента щели dx в точку наблюдения, теперь можно записать так

.

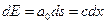В центре дифракционной картины, колебания от всех зон щели происходят в фазе. Результирующее колебание будет иметь амплитуду 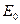, равную алгебраической сумме амплитуд колебаний от всех зон:

.

Отсюда следует, что постоянная

.

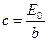Теперь амплитуду колебания от элементарной зоны dx можно представить так:

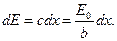
Вернёмся к произвольной точке Р на экране наблюдения. Рассмотрим колебания, приходящие в эту точку от центральной зоны щели (х = 0) и от элементарной зоны dx, отстоящей от центра на расстоянии х. Это второе колебание в точке наблюдения Р будет происходить со сдвигом по фазе относительно первого (см. рис. 8.1)

.

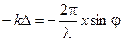Колебание, возбуждаемое в точке Р элементарной зоной с координатой х, можно записать теперь в следующем, окончательном виде:

. (8.2)

Проинтегрируем (8.2) по всей ширине щели

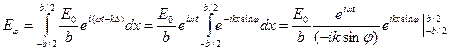. (8.3)

,

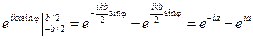где: .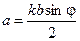

Воспользуемся формулой Эйлера:

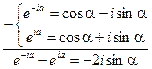
Эту разность двух экспонент используем в уравнении 8.3.

.

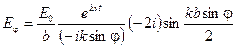Упростим это уравнение:

.

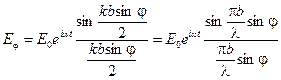Вернёмся от комплексной формы записи колебаний в точке Р к тригонометрической:

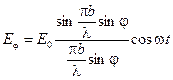. (8.4)

Амплитуда результирующего колебания в точке наблюдения Р

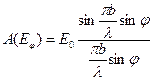. (8.5)

Проанализируем полученный результат.

В случае, когда

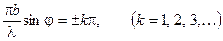(8.6)

амплитуда колебаний обращается в ноль. Это условие минимумов дифракции Фраунгофера от щели.

Условие минимумов b sinφ = k λ дифракции от щели имеет простое графическое истолкование (рис. 8.2).

Рис. 8.2

При выполнении этого условия, разность хода волн, излученных элементарными зонами, прилегающими к краям щели, будет равна целому числу длин волн (например, на рис. 8.2 b sinφ = λ).

В этом случае ширина щели может быть разделена на чётное число зон Френеля. Волны от соседних зон будут приходить в точку наблюдения в противофазе. Таким образом, волны попарно будут гасить друг друга.

Интенсивность колебания, как и всегда, пропорциональна квадрату амплитуды, то есть

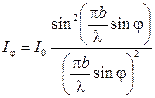. (8.7)

Здесь І₀ — интенсивность нулевого максимума в центре дифракционной картины.

Дифракционная картина симметрична относительно центра линзы, то есть

І_φ = І_-φ

Как было установлено (см. 8.6), направлениям φ, отвечающим условию

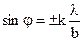
соответствуют «нулевые» минимумы дифракции.

График функции (8.7) приведён на рис. 8.3.

Рис. 8.3

Теперь, воспользовавшись методом графического сложения амплитуд, вычислим относительные интенсивности максимумов дифракционной картины от щели.