Метод векторных диаграмм. Зоны Френеля

Оставим на время интеграл Френеля (7.2) и поясним суть принципа Гюйгенса-Френеля на примере «осесимметричной задачи» дифракции (рис.7.6).

Рис. 7.6

S — первичный источник сферических волн, P — точка наблюдения.

Радиусом a = SО выделим фрагмент сферической волновой поверхности. Волновую поверхность разделим на кольцевые зоны — зоны Френеля. Первую зону — сферический сегмент — выделим радиусом . Здесь b — расстояние от вершины (полюса) волновой поверхности — точки О до точки наблюдения P.

Остальные зоны будем вырезать на сферической волновой поверхности, увеличивая каждый раз радиус от точки P на .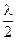

Таким образом, расстояние от внешнего края m-ой зоны до точки P составит величину

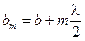(7.3)

Смысл деления волновой поверхности на такие зоны состоит в том, что колебания, приходящие в точку P от «сопряжённых» точек двух соседних зон, происходят в противофазе. Поэтому и результирующие колебания в точке P от двух соседних зон будут иметь сдвиг по фазе на π.

Как следует из уравнения Френеля (7.2), амплитуда вторичных колебаний пропорциональна площади зоны. Покажем, что для не слишком большого числа зон Френеля (m), площади всех зон примерно одинаковы (рис. 7.7).

Рис. 7.7

Выделим на волновой поверхности m зон Френеля. Площадь m-ой зоны

∆S_m = S_m – S_m-1.

Здесь S_m и S_m-1 — площади сферических сегментов, содержащих соответственно (m) и (m-1) зону.

Из рисунка 7.7 следует

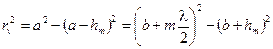(7.4)

Отсюда нетрудно вычислить высоту сферического сегмента

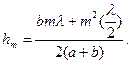
Пренебрегая слагаемым, содержащим λ², получим:

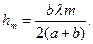(7.5)

Площади сферических сегментов:

,

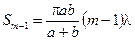
Теперь ясно, что площадь m-ой кольцевой зоны Френеля

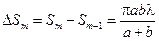(7.6)

Полученный результат свидетельствует о том, что площадь зоны не зависит от её номера — m. Это означает, что площади зон Френеля приблизительно одинаковы.

Попутно отметим, что из уравнения (7.4) можно получить выражение для радиуса m-ой зоны

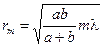(7.7)

Вернёмся к интегралу Френеля (уравнение 7.2)

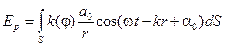
Рассмотрим его отдельно для каждой из зон. С ростом номера, как было показано, площадь зоны не меняется, но растёт расстояние 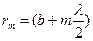и уменьшается коэффициент k(φ) (с увеличением φ). В результате, с ростом номера зоны амплитуды соответствующих колебаний в точке P будут монотонно убывать:

E₁ > E₂ > E₃ >…>…

Учитывая, что колебания от двух соседних зон в точке наблюдения происходят в противофазе, амплитуду результирующего колебания можно представить в виде:

E_P = E₁ – E₂ + E₃ – E₄ +…

Или так:

(7.8)

Амплитуды с ростом номера зоны монотонно убывают, поэтому можно принять, что 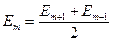Отсюда следует, что все скобки в выражении (7.8) равны нулю.

Амплитуда колебания, создаваемого в точке P всеми вторичными источниками сферической волновой поверхности:

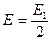
Эта амплитуда вдвое меньше амплитуды того колебания, которое создаётся в точке P вторичными источниками только одной первой зоны (!). Если открыта не вся волновая поверхность, а только m зон, то результирующая амплитуда:

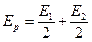— при нечётном m

и

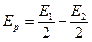— при чётном m.

Более детально эту задачу можно решить, воспользовавшись методом векторных диаграмм.

Разобьём зоны Френеля на сферической волновой поверхности на большое число «подзон». Каждая зона Френеля, таким образом, будет разделена на большое число элементарных кольцевых полосок. В точке наблюдения эти подзоны будут создавать колебания, сдвинутые по фазе на малую долю π. Сложим эти колебания, используя метод векторных диаграмм (рис. 7.8)

Рис. 7.8

На рисунке 7.8 модуль каждого вектора равен амплитуде колебаний, приходящих в точку P от соответствующей подзоны. И каждый вектор повёрнут относительно предыдущего на угол, равный разности фаз этих соседних колебаний.

Учитывая, что с ростом номера подзоны амплитуда колебаний падает, в результате сложения колебаний получим не замкнутую линию, а ломаную спираль. При увеличении числа подзон и, соответственно, уменьшении их площади, ломаная спираль будет стремиться к гладкой (рис. 7.9).

Рис. 7.9