Интенсивность дифракционной картины
Вновь разделим поверхность щели на узкие полоски, параллельные её краям. Но теперь проследим за тем, чтобы все эти подзоны были одинаковой площади. В этом случае вторичные волны, излучаемые полосками, будут иметь одинаковые амплитуды ΔА.
Каждая следующая волна, кроме того, будет иметь неизменный сдвиг по фазе относительно предыдущей. Величина фазового сдвига будет зависеть от угла φ.
Сложим графически все эти волны в максимуме нулевого порядка (φ = 0). Здесь все волны собираются в фазе. Соответствующая векторная диаграмма приведена на рис. 8.4.

Рис. 8.4
Эта сумма равна А0. Особо отметим очевидный, но важный факт: амплитуда результирующего колебания А0 равна сумме модулей векторов 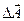 .
.
Обратимся теперь к направлению(φ1), соответствующему первому максимуму.
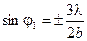
Этому направлению отвечает разность хода волн от краёв щели, равная 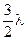 :
:
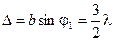
Это означает, что щель может быть поделена на 3 зоны Френеля. Две из них погасят друг друга, а третья обеспечит максимум номер 1 (первый дифракционный максимум).
Соответствующая векторная диаграмма (спираль) приведена на рис. 8.5.

|

Рис.8.5
Вспомним «очевидную, но важную деталь»: длина этой спирали – по-прежнему А0, т.е.
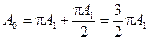
Следовательно, 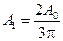 .
.
Вычислим амплитуду второго максимума. Его условие:
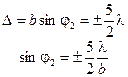
Спираль, отвечающая первому максимуму, имела полтора витка (см. рис. 8.5).
А теперь подобная же векторная диаграмма будет иметь уже два с половиной витка (при той же длине А0!)
Значит, полная длина спирали в два с половиной оборота будет равна
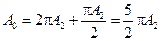
Таким образом, во втором максимуме амплитуда колебания составит такую величину:
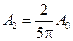
Итак,
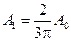 ,
, 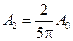
Легко догадаться, не производя вычислений, что в третьем максимуме амплитуда
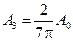 ,
,
затем
 .
.
И так далее.
Интенсивности колебаний в максимумах будут соотноситься как квадраты амплитуд, то есть: 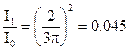 ,
, 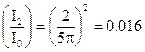 ,
, 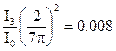
С увеличением номера максимума интенсивность быстро уменьшается, то есть основная энергия, прошедшая с волной сквозь щель, локализуется в «нулевом» центральном максимуме (рис. 8.3).
Вычислим теперь угловую ширину центрального максимума (см. рис. 8.3). Он ограничен первыми минимумами, условия которых известны:
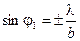 .
.
Отсюда угловая ширина нулевого максимума
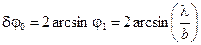 .
.
При малом угле 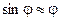 , поэтому
, поэтому
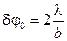 .
.
Дата добавления: 2015-08-04; просмотров: 963;

