Критерий типа дифракции
Для того чтобы наблюдать дифракцию Фраунгофера — дифракцию в параллельных пучках, нам пришлось поставить за щелью собирающую линзу.
Но уже на интуитивном уровне понятно, что при малой ширине щели (b) и значительном расстоянии до экрана (l), дифракцию Фраунгофера можно получить и без линзы.
Так в каких же случаях возникает тот или иной тип дифракции?
Для ответа на этот вопрос обратимся к рис. 8.6.

Рис. 8.6
Здесь Δ —разность хода волн от краёв щели.
Напомним, что в случае дифракции в параллельных пучках (Фраунгофера) эта разность хода равна
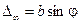 (8.8)
(8.8)
Теперь вычислим эту величину в общем случае, воспользовавшись теоремой косинусов (см. рис. 8.6)
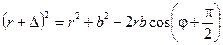 .
.
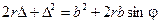
На этом этапе уместно пренебречь малой величиной высшего порядка — 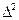 , так как
, так как  . Тогда разность хода волн, пришедших в точку наблюдения от краев щели, можно записать так:
. Тогда разность хода волн, пришедших в точку наблюдения от краев щели, можно записать так:
 . (8.9)
. (8.9)
При r → ∞, формула (8.8) приводит к разности хода, соответствующей дифракции Фраунгофера (8.7).
Заменяя в расчёте реальную разность хода (8.8) «идеальной» (8.7), мы соглашаемся с погрешностью
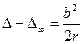
Если 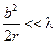 , то речь идёт о дифракции Фраунгофера.
, то речь идёт о дифракции Фраунгофера.
Когда 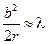 — это дифракция Френеля.
— это дифракция Френеля.
В качестве критерия типа дифракции принято использовать безразмерный параметр
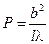
где: l — расстояние от щели до экрана.
При изменении ширины щели (b), расстояния до экрана (l) или длины волны (λ), в общем случае будет меняться и величина параметра Р.
Характер дифракционной картины, возникающей за щелью на экране, связан с величиной этого безразмерного параметра 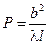 следующим образом
следующим образом
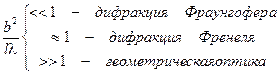
Этот результат имеет интересное геометрическое толкование (рис. 8.7).

Рис. 8.7
Если из точки наблюдения P мы видим в плоскости щели m зон Френеля, то
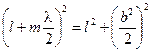
Отсюда следует: 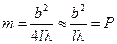 .
.
Здесь мы пренебрегли слагаемым 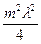 по сравнению с
по сравнению с 
Таким образом, безразмерный параметр Р связан с числом зон Френеля в плоскости щели.
m = P « 1 — дифракция Фраунгофера,
m = P ≈ 1 — дифракция Френеля,
m = P » 1 — геометрическая оптика.
Если щель открывает только малую долю центральной зоны Френеля — на экране дифракция Фраунгофера с соответствующим распределением максимумов и минимумов (рис. 8.3).
Если в плоскости щели помещается небольшое число зон Френеля – на экране возникнет дифракция Френеля: по краям изображения щели будут видны тёмные и светлые полосы.
В случае большого числа зон Френеля в плоскости щели, её изображения на экране можно построить, используя методы геометрической оптики.
Итог лекции 8.
1. Дифракция Фраунгофера от длинной щели. 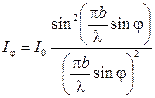
2. Критерий типа дифракции. 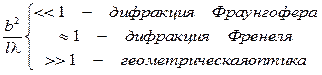
Лекция 9 «Дифракционная решётка
как спектральный прибор»
План лекции:
1. Краткий обзор предыдущих лекций.
1.1 Критерий типа дифракции.
1.2 Дифракция Фраунгофера от щели.
1.3 Многолучевая интерференция.
2. Дифракционная решётка как спектральный прибор.
3. Критерий Рэлея. Разрешающая способность дифракционной решётки.
Итог лекции 9
Дата добавления: 2015-08-04; просмотров: 1376;
