Способы наблюдения интерференции света
Интерференцию света можно наблюдать только при наложении когерентных волн. Это должны быть волны одинаковой частоты, с неизменной разностью начальных фаз. Получение таких волн – непростая экспериментальная задача. Обычно с этой целью исходную волну искусственно разделяют на две. Так возникают две когерентные волны. При их последующем слиянии можно наблюдать явление интерференции.
Познакомимся подробнее с некоторыми классическими методами получения когерентных волн.
Зеркала Френеля (1816 г.) (рис. 5.3)

Рис. 5.3
Источник света S — ярко освещенная узкая щель; ON и OM — плоские зеркала, образующие угол близкий к 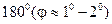 ; Э1 — ширма, предохраняющая экран наблюдения (Э) от попадания прямых лучей света от источника S;
; Э1 — ширма, предохраняющая экран наблюдения (Э) от попадания прямых лучей света от источника S;
S1, S2 — мнимые изображения источника света S в зеркалах ОМ и ОN соответственно.
Так как <POQ = 2φ, а точки S, S1 и S2 лежат на одной окружности радиуса r = OS = OS1 = OS2, расстояние между мнимыми источниками S1 и S2
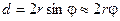
Расстояние от мнимых источников до экрана:
l = a + b ≈ r + b.
Здесь а — расстояние от мнимых источников до ребра зеркал: 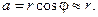
Теперь, воспользовавшись уравнением 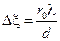 (5.10), вычислим ширину интерференционных полос на экране наблюдения.
(5.10), вычислим ширину интерференционных полос на экране наблюдения.
В нашем случае
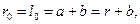 а
а 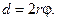
Значит ширина интерференционных полос, даваемых зеркалами Френеля,
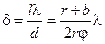 .
.
Возможное число полос:
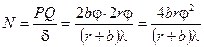 .
.
 На рисунке 5.4 приведена еще одна схема установки «Зеркала Френеля».
На рисунке 5.4 приведена еще одна схема установки «Зеркала Френеля».

Рис. 5.4
Бипризма Френеля (рис. 5.5)
Две призмы с малыми преломляющими углами J, сложенные своими основаниями, образуют бипризму (рис.5.5).


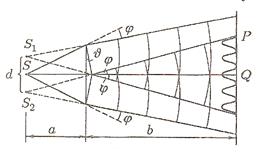
Рис. 5.5.
Бипризма освещается светом прямолинейного источника S, параллельного общей грани бипризмы. Известно, что при прохождении призмы, световые лучи отклоняются в сторону ее основания на угол φ = (n - 1) 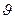 . Здесь n – показатель преломления материала призмы
. Здесь n – показатель преломления материала призмы
В результате преломления, возникают два мнимых источника S1 и S2 — изображения реального источника света S.
Расстояние между мнимыми источниками S1 и S2
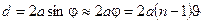 ,
,
где: a — расстояние от источника S до бипризмы.
Интерференционная картина возникает в результате суперпозиции двух когерентных цилиндрических волн, исходящих из мнимых линейных источников S1 и S2.
Для расчета ширины интерференционных полос вновь воспользуемся уравнением
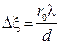 (5.10)
(5.10)
В случае бипризмы: r0 = (a + b), 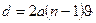 .
.
Поэтому ширина интерференционных полос:
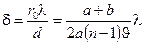 .
.
Число интерференционных полос, как и в случае зеркал Френеля, найдем, разделив ширину области перекрытия световых пучков 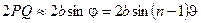 на ширину интерференционных полос.
на ширину интерференционных полос.
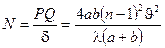 .
.
Дата добавления: 2015-08-04; просмотров: 1324;
