Краткий обзор предыдущих лекций. Метод векторных диаграмм

Две последние лекции были посвящены изучению явления интерференции. В чём состоит это явление, которое возникает при наложении волн?

Прежде всего, необходимо напомнить, что интерференцию можно наблюдать при сложении только когерентных волн. Две векторные волны когерентны, если они удовлетворяют следующим условиям:

1. Частоты волн должны быть одинаковыми ω₁ = ω₂ = ω.

2. Разность их начальных фаз не должна меняться со временем

ΔФ₀ = Ф₀₁ - Ф₀₂ = const ≠ f(t)

3. Угол между плоскостями поляризации волн также должен оставаться неизменным. В дальнейшем мы рассматриваем волны, поляризованные в одной плоскости.

Пусть источники S₁ и S₂ излучают когерентные волны

S₁ = A₁cos (ωt - kr₁ - Ф₀₁) = A₁cos (ωt - φ₁),

S₂ = A₂cos (ωt - kr₂ - Ф₀₂) = A₂cos (ωt - φ₂).

Здесь φ_i = kr_i + Ф_0i .

Согласно принципу суперпозиции при сложении таких волн возникает волна той же частоты, что и складываемые волны

S = S₁ + S₂ = Acos (ωt - φ)

Амплитуда A и фаза φ новой волны определяется амплитудами и фазами исходных волн

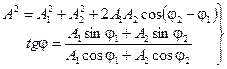(6.1)

Каждая волна в заданной точке пространства реализуется в виде колебания. Таким образом, задача сложения двух волн в точке наблюдения — Р сводится к известной задаче сложения двух колебаний. Часто при решении подобной задачи используют «метод векторных диаграмм». Этот же метод мы используем и при сложении не двух, а N когерентных волн.