Волновая область. Волновой параметр

Обсуждая явление интерференции, мы не раз оговаривались, что будем рассматривать сложение когерентных волн в дальней «волновой» зоне.

Где начинается эта область? На сколько должна быть удалена точка наблюдения от источников, чтобы можно было считать, что она находиться в волновой зоне?

Обратимся к рисунку 6.3. На рисунке представлен фрагмент той решётки из N вибраторов, которую мы только что обсуждали. Здесь ОР = r₀ — расстояние от точки наблюдения (Р) до середины линейной решётки.

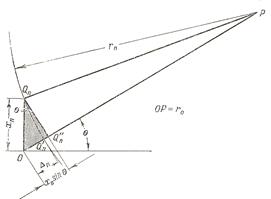
Рис. 6.3

Истинная разность хода волн от центрального (О) и n-ого источника

Δ_n = r₀ - r_n

Из треугольника OQ_nP следует

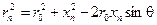
Таким образом

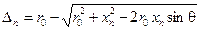
или

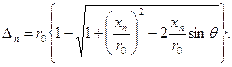(6.9)

Это истинная разность хода; мы же принимаем в расчётах

. (6.10)

Такую подмену можно считать допустимой, если возникающая при этом погрешность разности фаз мала по сравнению с π, или погрешность разности хода значительно меньше :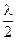

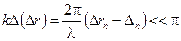или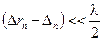

Разложим радикал (6.9) в ряд с остаточным членом по формуле

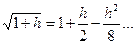
В нашем случае

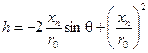
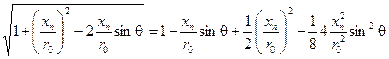
Теперь истинную разность хода с точностью до малой величины порядка 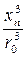можно записать так (6.9)

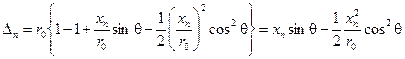
Разность 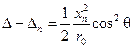должна быть значительно меньше :

.

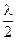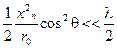Это условие должно выполняться для всех углов θ, т.е.

.

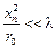Отсюда следует, что расстояние от источников до «волновой зоны» должно удовлетворять условию

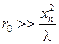(6.11)

Возьмём наибольшее значение 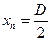, где D — общий размер линейной решётки источников. Тогда условие (6.11) можно записать в виде

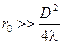(6.12)

Безразмерное выражение 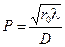называется волновым параметром.

Для волновой зоны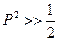

Наши приближённые расчёты можно считать справедливыми, если волновой параметр заметно превышает единицу P >> 1.