Многолучевая интерференция

Рассмотрим N когерентных источников одинаковой мощности, расположенных на одной прямой (рис.6.1).

Рис. 6.1

Расстояния между источниками одинаковы и равны d. Угол 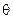определяет направление от источников на точку наблюдения Р. Эта точка столь удалена, что направления от источников на эту точку можно считать параллельными прямыми.

В этой удалённой точке разность хода волн, приходящих от двух соседних источников, равна

Δ = d sin θ. (6.2)

Таким образом, в точке наблюдения мы будем складывать N колебаний одинаковой амплитуды. Но по фазе колебания от двух соседних источников будут отличаться на

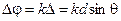(6.3)

Сдвиги по фазе относительно первого источника образуют арифметическую прогрессию:

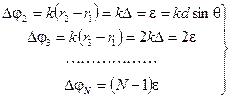(6.4)

Сложим все эти колебания, воспользовавшись методом векторных диаграмм. В данном случае диаграмма - ломаная, состоящая из N звеньев одинаковой длины А. Каждое звено при этом повёрнуто относительно предыдущего на угол ε (рис. 6.2)

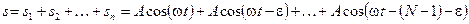
В результате суперпозиции этих N колебаний одинаковой частоты возникнет новое колебание той же частоты:

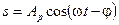(6.5)

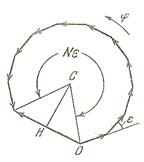
Рис. 6.2.

Амплитуда этого результирующего колебания, как следует из диаграммы

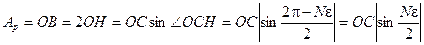(6.6)

Здесь расстояние ОС можно связать с амплитудой отдельного колебания А:

(6.7)

Объединив результаты (6.6) и (6.7), получим

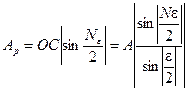
Интенсивность колебаний (волны) в точке наблюдения Р пропорциональна квадрату амплитуды:

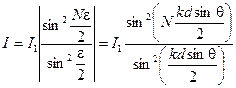(6.8)

Здесь: 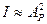— интенсивность результирующего колебания;

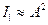— интенсивность колебания, связанного с прохождением через точку Р волны от одного из источников.

Проанализируем полученный результат.

Как следует из уравнения (6.8), интенсивность волны, возникающей при сложении N когерентных волн, зависит только от направления θ.

При 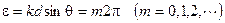числитель и знаменатель обращаются в ноль. Раскроем эту неопределённость, дважды воспользовавшись правилом Лопиталя.

Значит, при ε = k d sinθ = 0, ±2π, ±4π,… в соответствующей точке наблюдения возникает максимум, интенсивность которого в 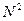раз превышает интенсивность отдельных волн.

Это главные максимумы 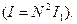Их можно наблюдать в направлениях, определяемых следующими углами

ε = k d sinθ = ±2mπ,

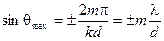, m = 0, 1, 2,…

В этих направлениях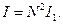

Между двумя главными максимумами — (N – 1) промежуточный минимум.

Условия минимумов:

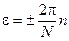
где: n — целые числа, за исключением кратных N.