Интерференционные полосы равной толщины (кольца Ньютона)
Интерференционные полосы равной толщины наблюдаются, например, в воздушной прослойке между плоским стеклом и лежащей на нем плоско-выпуклой линзой (рис. 5.6). При нормальном падении, свет частично отражается от сферической поверхности линзы, а частично проникает в воздушный клин и отражается от плоской пластины.
Разность хода этих двух когерентных волн равна удвоенной толщине воздушного клина Δ = 2h.
Вычислим толщину воздушного клина h. Как видно из рисунка
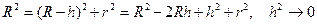 .
.

Рис.5.6
Отсюда следует:  , где R — радиус кривизны линзы.
, где R — радиус кривизны линзы.
Учитывая, что при отражении от оптически более плотной среды, фаза волны скачком меняется на π, вычислим разность фаз волн, отраженных от линзы и пластины:
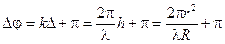
Эта разность фаз будет меняться по мере удаления от центра линзы. В связи с этим возникает чередование светлых и темных полос (рис. 5.7)


Рис. 5.7
В точках, для которых разность фаз кратна 2π, возникнут максимумы:
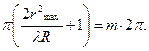
Вычислим теперь радиусы светлых колец
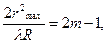
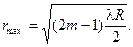
Условие минимума — условие возникновения темных колец:
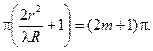
Радиусы темных колец: 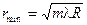 .
.
Дата добавления: 2015-08-04; просмотров: 872;
