Краткий обзор предыдущей лекции. При сложении двух световых волн, излучаемых независимыми источниками S1 и S1, возникает волна, амплитуда которой Eр сложным образом связана с амплитудами

При сложении двух световых волн, излучаемых независимыми источниками S₁ и S₁, возникает волна, амплитуда которой E_р сложным образом связана с амплитудами исходных волн E₁ и E₂.

,

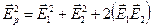
Это мгновенное значение напряженности в общем случае меняется с высокой частотой. В то же время приборы регистрируют среднее значение напряженности за время быстродействия прибора — τ.

.

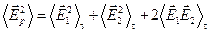В результате усреднения, было получено следующее выражение для интенсивности результирующей волны

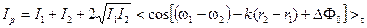(5.1)

При этом предполагается, что угол α между направлениями поляризации волн не меняется. В дальнейшем мы рассматривали волны, поляризованные в одной плоскости, т.е. когда α = 0. В этом случае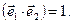

С тем, чтобы исключить зависимость интенсивности от времени, были сформулированы еще два условия, которым должны удовлетворять волны: частоты волн должны быть одинаковыми, а разность начальных фаз – постоянной.

Волны, удовлетворяющие этим трем условиям:

1.

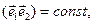
2. ω₁ = ω₂ = ω,

3. ,

называются когерентными.

В случае суперпозиции когерентных волн, уравнение (5.1) принимает такой вид:

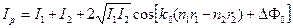(5.2)

Если волны распространяются в одной среде, т.е. n₁ = n₂ = n, уравнение (5.2) можно еще упростить

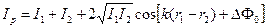(5.3)

Здесь: 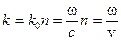— волновое число,

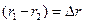— геометрическая разность хода волн.

В случае наложения волн одинаковой интенсивности (I₁ = I₂)

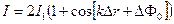. (5.4)

Теперь исследуем результат суперпозиции волн, когда r₁ и r₂ » d. Здесь d — расстояние между двумя когерентными источниками.

2. Сложение волн на «большом» расстоянии от источников

Строго понятие «большое расстояние» будет определено на следующей лекции. Сейчас мы будем считать удаление точки наблюдения от источников «большим», если расстояния r₁ и r₂ >> d. Например, расстояние между источниками световых волн d ~ λ ~ 10^-6 м, а результат их сложения будем оценивать на удалении r ~ (1-10) м. В этом случае r на 6 - 7 порядков превосходит d, а направления от источников волн - 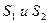на точку наблюдения будут практически параллельными.

Как было установлено (см. 5.4), интенсивность результирующей волны

.

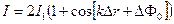(Здесь мы предположили, что мощности источников одинаковы, то есть I₁ = I₂).

В случае большого удаления точки наблюдения P, разность хода волн 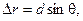где θ — угол, определяющий направление от источников на точку наблюдения (рис.5.1).

Теперь можно связать интенсивность интерференционной картины (I) с углом θ. 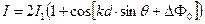. (5.5)

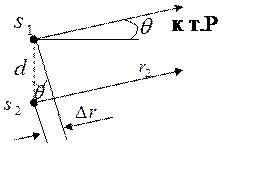
Рис. 5.1
Максимумы интенсивности будут наблюдаться в направлениях 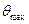, для которых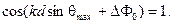

.

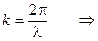
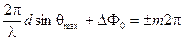Соответственно условие минимума выглядит так:

.

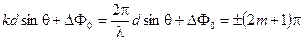В случае сложения синфазных волн, то есть когда Φ₀₁ = Φ₀₂ и ΔΦ₀ = 0,

.

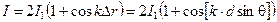Теперь условия максимума и минимума интенсивности принимают особенно простой вид.

Условие максимума:

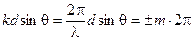. (5.6)

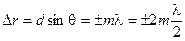. (5.7)

Максимум интерференции наблюдается в направлениях, удовлетворяющих условию:

.

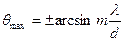Для этих направлений разность хода волн равна целому числу длин волн или четному числу полуволн (5.7).

Условие минимума:

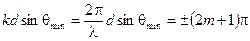. (5.8)

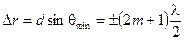. (5.9)

Интерференционные минимумы можно наблюдать в направлениях 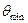, для которых разность хода волн равна нечетному числу полуволн (5.9).

Распределение интенсивности при интерференции двух когерентных волн приведено на рисунке 5.2

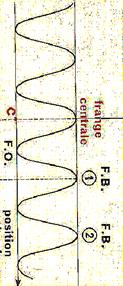
Рис. 5.2

Вычислим ширину интерференционной полосы, то есть расстояние между двумя соседними минимумами (или максимумами) интерференционной картины.

Учитывая малость угла θ, можно условие m-го минимума записать так:

.

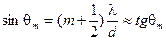Условие следующего, (m + 1)-го минимума:

.

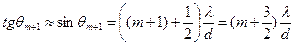Координата (m + 1)-го минимума:

.

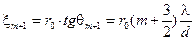Координата предыдущего m – го минимума:

.

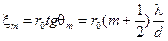Ширина интерференционной полосы:

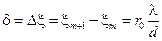. 5.10

На рисунке 5.2 ширина интерференционной полосы (δ) — расстояние между двумя соседними максимумами. Покажите, что это расстояние совпадает и с расстоянием между двумя минимумами, ограничивающими максимум.