Особенности суперпозиции световых волн. Когерентность

Рассмотрим теперь суперпозицию двух векторных световых волн.

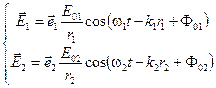
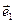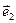Здесь и — единичные векторы, определяющие поляризацию волн.

В результате сложения этих волн, согласно принципу суперпозиции,

.

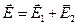Значит интенсивность результирующей волны, пропорциональная квадрату амплитуды, может быть представлена так:

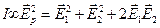. (4.6)

Заметим, что частота колебаний в световой волне порядка ω ~ 10¹⁴ с^-1, а период, соответственно, — Т ~ 10^-14с. Не существует приборов, способных измерять мгновенные значения столь быстро меняющегося параметра. Прибор будет регистрировать лишь среднее значение напряженности за время быстродействия прибора — τ (τ >> Т).

Усредним слагаемые уравнения (4.6)

.

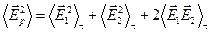Итак, начнем почленно усреднять:

.

Здесь аргумент косинуса 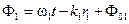меняется с высокой частотой ω, поэтому

.

Тот же результат получим и для второго слагаемого:

.

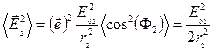Прежде чем анализировать результат усреднения третьего (интерференционного) слагаемого перепишем его несколько иначе:

.

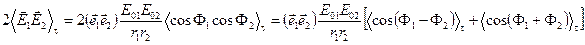Скалярное произведение единичных векторов равно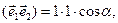

где: α — угол между направлениями поляризации волн.

Для того чтобы наблюдатьустойчивую интерференционную картину, необходимо, чтобы этот угол не менялся во времени: α ≠ ƒ(t).

В дальнейшем мы будем рассматривать сложение волн, поляризованных в одной плоскости. Для таких волн α = 0 и cosα = 1.

Далее отметим, что аргумент косинуса

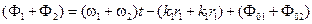
меняется во времени с высокой частотой 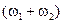. Поэтому среднее значение

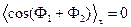
Обратимся теперь к разности фаз .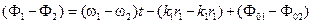

Чтобы освободиться от временной зависимости интенсивности и иметь устойчивое во времени пространственное интерференционное перераспределение энергии, нужно

1) чтобы частоты волн были одинаковыми, то есть 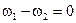, и

2) чтобы разность начальных фаз оставалась постоянной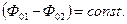

Волны, отвечающие этим условиям, называются когерентными.