Суперпозиция двух сферических гармонических синфазных волн

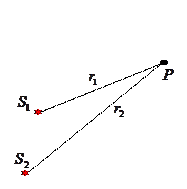Два источника S₁ и S₂ синфазно излучают сферические волны одинаковой амплитуды 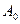и частоты ω. В точке наблюдения Р их можно записать так (рис. 4.1):

.

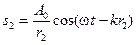Рис. 4.1

Важно отметить, что r₁ и r₂ — неизменные, постоянные расстояния от источников до точки наблюдения Р. Одинаковые начальные фазы волн приняты равными нулю.

Тогда колебания в точке Р, связанные с волнами S₁ и S₂, можно представить следующими уравнениями:

, (4.1)

где:

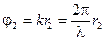
Волны S₁ и S₂ в точке Р представляют собой колебания.

Сложение волн в заданной точке превращается, таким образом, в знакомую задачу сложения колебаний с амплитудам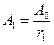и и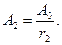

В результате сложения двух колебаний одинаковой частоты, в точке наблюдения Р возникает новое колебание той же частоты:

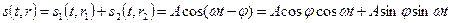. (4.2)

Амплитуда А и фаза φ этого нового колебания связаны с амплитудами и фазами складываемых колебаний:

,

.

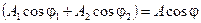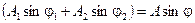Отсюда следует:

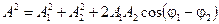(4.3)

и

. (4.4)

К такому же результату можно прийти, воспользовавшись известным методом векторных диаграмм (рис.4.2).

.

,

.

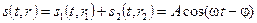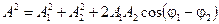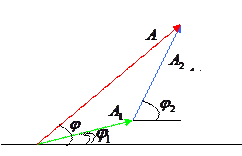
Рис. 4.2

Интенсивность волны, как известно, пропорциональна квадрату ее амплитуды

I = α A², это позволяет переписать результат (4.3) в следующем виде:

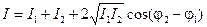(4.5)

Этот последний результат свидетельствует о том, что суммарная интенсивность при сложении двух волн существенно зависит от разности их фаз

.

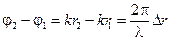В точках пространства, для которых 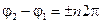, (n = 0, 1, 2, 3...), интенсивность суммарной волны превосходит сумму интенсивностей исходных волн

.

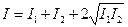Если происходит сложение волн одинаковой интенсивности (I₁ = I₂), то интенсивность суммарной волны в этих точках вдвое превышает суммарную интенсивность отдельных волн:

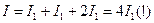
Но наряду с этим, в соседних точках, где разность фаз 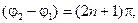при суперпозиции волн возникает волна, интенсивность которой меньше суммы интенсивностей складываемых волн:

.

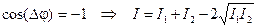Если I₁ = I₂, то в результате сложения волн интенсивность в этих точках оказывается равной нулю.

Таким образом, при наложении, суперпозиции волн происходит пространственное перераспределение их энергии. В этом перераспределении и состоит суть явления интерференции.