Повторим условия когерентности.

Волны когерентны, если:

1. их частоты одинаковы,

2. разность их начальных фаз постоянна и

3. угол между направлениями поляризации волн остается постоянным .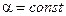

Напомним, что мы будем рассматривать частный случай, когда волны поляризованы в одной плоскости: .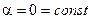

Вернемся к среднему значению третьего (интерференционного) слагаемого. Теперь его можно переписать в таком виде:

.

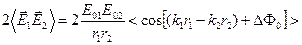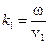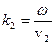Здесь волновые числа складываемых волн и зависят от скорости волн в разных средах. Как известно, скорость распространения света в среде 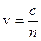, где n — показатель преломления среды. Тогда

где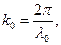

λ₀ — длина волны в вакууме, одинаковая для обеих волн.

Произведение геометрического хода волны r₁ на показатель преломления среды n₁ называется оптическим ходом волны (r_1* n₁).

Значение интерференционного слагаемого зависит от разности оптического хода волн.

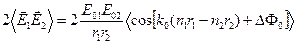
Если волны распространяются в одной и той же или в одинаковых средах, то n₁ = n₂ = n и .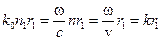

Этот вывод будет справедлив и для второй волны: .

Тогда уравнение (4.6) окончательно можно представить в таком виде:

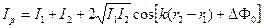. (4.7)

Интерференционная картина будет иметь наибольшую контрастность, если интенсивность волн будет одинаковой I₁ = I₂ = I₀. Тогда результирующая интенсивность равна

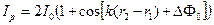. (4.8)

Результат (4.8) еще более упростится, если в пространстве перекрываются волны от двух синфазных источников. Это означает, что

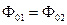или .

Интенсивность результирующей волны в этом случае можно записать так:

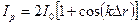. (4.9)

Здесь – волновое число, разность хода волн.

Условие интерференционного максимума (см.4.9):

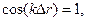
то есть 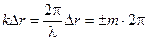, где m = 0, 1, 2, 3,…

В этом случае разность хода волн .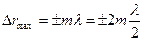

Максимум наблюдается в тех точках, для которых разность хода ∆r равна целому числу длин волн (четному числу полуволн).

Условие интерференционного минимума (I = 0) (см.4.9):

то есть 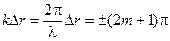или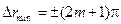

При суперпозиции когерентных волн возникает минимум, когда разность их оптического хода равна нечетному числу полуволн.