Лекция 29
РАСЧЕТ ПЛАСТИН МЕТОДОМ РИТЦА-ТИМОШЕНКО
При использовании прямых методов задача, сформулированная в дифференциальных уравнениях, сразу сводится к системе алгебраических уравнений.
Если задана функция у(х).
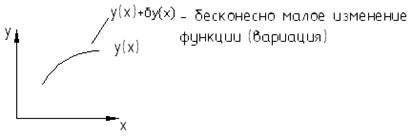

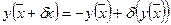
δ- бесконечно малая.
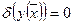
Т. Лагранжа- Лежен- Дирихле: устойчивому состоянию упругой системы соответствует минимуму ее полной потраченной энергии.
Полная потраченная энергия системы вычисляется по формуле:
Э=А-U (1)
Где А – работа внешней нагрузки, U- работа внутренних усилий.
! Перемещение совпадает с направление силы
U: сила совершает работу на перемещение, противоположное их направлению.
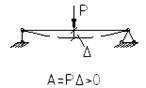
Для А и U имеются формулы для балок, пластинок и оболочек.
Для пластинок:
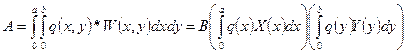 =>
=>
Если q(x,y)=q(x)q(y) – разделения переменных
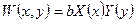 (2)
(2)
Где, В- искомая амплитуда прогиба, Х(х), Y(y)- аппроксимирование функции по каждому их направлению.
Если переменная разделяется функцией q и функцией W.
Для пластинок работы внутренних усилий равна: 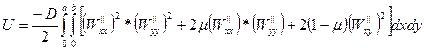
Где 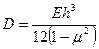 .
.
Если W(x,y) можно принять в виде (2), то:
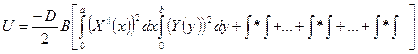
Вычитаем вариацию от полной потенциальной энергии:
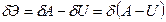
С точности до бесконечно малых высшего порядка вариации функций равно первому дифференциалу: 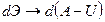
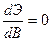 - минимальная полная потенциальная энергия
- минимальная полная потенциальная энергия
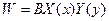
В - может меняться, Х(х), Y(y)- фиксированные функции, соответствующие граничным условия и нагружению.
Вычисляя данную производную, можно записать:
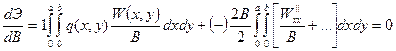
В результате получается линейное алгебраическое уравнение:
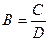
Тогда: 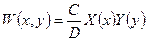 -
-
Предполагается, что задача будет решиться в безразмерном виде.
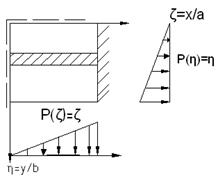
По методу Ритца-Тимошенко, основанного на т. Лагранжа- Лежен- Дирихле, необходимо задать функцию прогиба в виде:
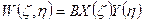
Строим аппроксимированную функцию х(ζ): вырезаем полоску по направлению рассматриваемой оси ζ, рассматриваем ее как обыкновенную балку:
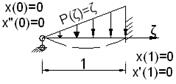
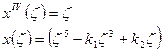
Аналогично строим аппроксимированную функцию у(η):
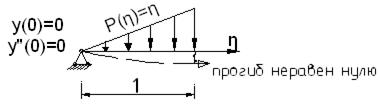
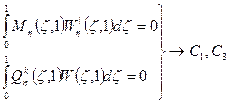
Данным граничным условиям должна удовлетворять функция 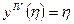
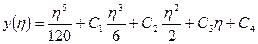
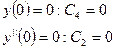
Подставляем выражение для Qη
После этого выражение для прогиба определено с точностью до параметра В.
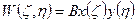
При решении задачи в безразмерном виде записывают следующее выражение для полной потенциальной энергии пластинки:
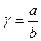 - отношение сторон пластинки
- отношение сторон пластинки


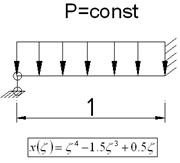
Построено статическим методом В.З. Власова. Тогда величины определенных интегралов:
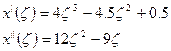
Вычисляем величины определенных интегралов, входящий в вр. 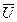
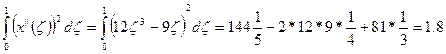
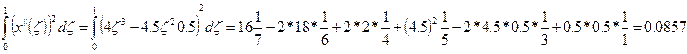
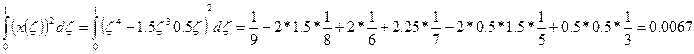
В результате выражения для 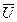 и
и 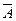 принимают вид:
принимают вид:
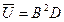
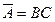
Далее зале записываются выражения:
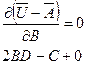
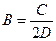 - амплитуда прогиба пластинки
- амплитуда прогиба пластинки
Тогда прогиб окончательно принимает вид:
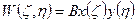
Затем необходимо записать в безразмерном виде выражения для изгибаемых моментов и поперечных сил:
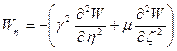
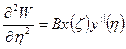
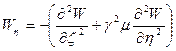
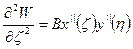
Выражения для поперечных сил:
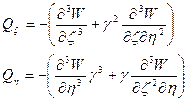
Рассмотрим некоторые вопросы, связанные с очертанием эпюр в пластинках. По заданию на расчет пластинок строят необходимо следующее:
 при
при 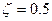 ,
, 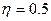
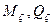 при
при 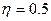
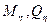 при
при 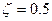
Необходимо сделать следующее: 
Вводим:
WRITE (‘B=’); READLN (B);
1: WRITE (‘KCI=’); READLN (KCI);
WRITE (‘ETA=’); READLN (ETA);
W:=B*(KCI*KCI* KCI* KCI-1.5* KCI* KCI* KCI+0.5* KCI)* (ETA*….);
WRITELN(‘W=’,W); GOTO1;
Если прописать в W: Mζ=…, Mη=…, Qζ=…, Qη=…
ζ=0; 0.25; 0.5; 0.75; 1
η=…
В результате получаются эпюры характерного очертания:
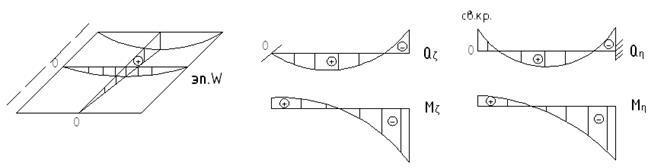
Дата добавления: 2015-08-01; просмотров: 759;
