Лекция 30

Расчет пластинок методом Бубнова-Галеркина.

Записываем дифференциальное уравнение изгиба элемента пластинки:

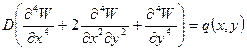(1)

Для конкретной задачи записывается по два граничных условия в каждой точке.

Записываем дифференциальное уравнение в безразмерном виде: при этом расчет одной пластины соответствует бесконечному множеству реальных пластин.

Вводим безразмерные переменные и функции по следующим формулам:

,

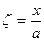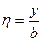
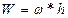
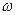- безразмерный параметр прогиба; 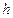- толщина (м).

,

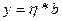
Подставляя данные формулы в уравнение (1):

/:

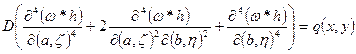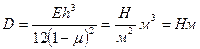
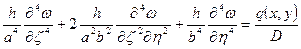
Вводим параметр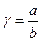

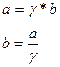
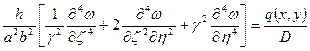
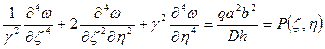(2)

- дифференциальное уравнение изгиба пластинки в безразмерном виде.

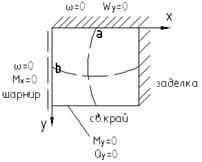
При этом пластинка примет вид:

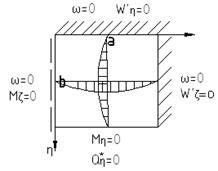
В безразмерном виде формулы для внутренних силовых факторов примут вид:

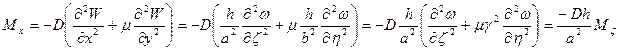
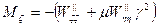- безразмерный изгибающий момент в направлении оси ζ.

Для оси η:

-

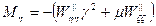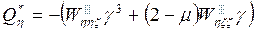
В уравнении (2) справа от знака “=”- внешние силы, а слева- внутренние.

Принцип Лагранжа: Сумма работ всех внешних и внутренних сил упругой системы на любом возможном и бесконечно малом перемещении равно 0.

Возможные перемещения должны быть совместимы с граничными условиями задач.

Применяем принцип Лагранжа к уравнению (2).

Возможное перемещение обозначим: .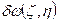

В методе Бубнова-Галеркина прогиб в первом приближении решения записаться в виде:

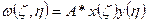
А- амплитуда прогиба, максимальное из решения задач по методу Бубнова-Галеркина.

Вариации прогиба записываются в виде:

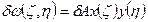
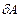- бесконечно малое изменение амплитуды прогиба.

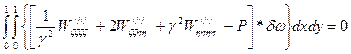(3)

В результате подстановки 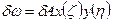можно записать:

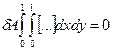
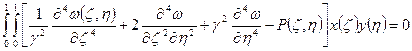
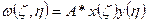- функция с разделяющимися переменными

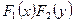- функция с разделяющимися переменными

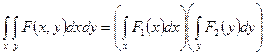
Тогда получаем следующие выражения:

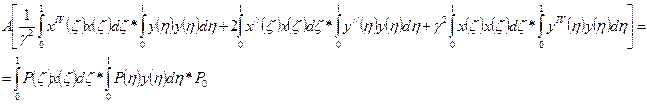
Т.к. функци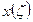и и 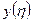известны, то известны все величины определенных интегралов. После чего можно записать:

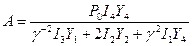
где 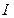и 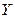моменты инерции.

После нахождения амплитуды прогиба все величины в пластинке подсчитываются по следующим формулам:

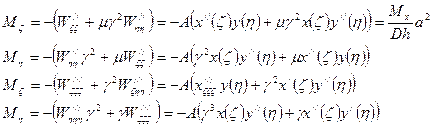
Аналогичные формулы для этих параметров используются методом Рицце - Тимошенко.

Рассмотрим пример:

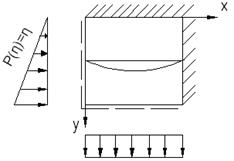
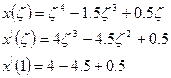
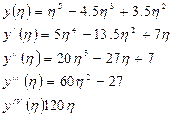
Получаем выражения для следующих производных функций

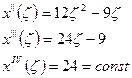
Подсчитаем интеграл: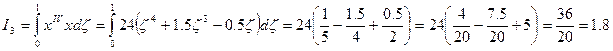

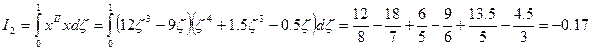
Аналогично вычисляются интегралы I₁ и I₄.

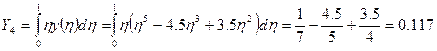
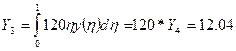
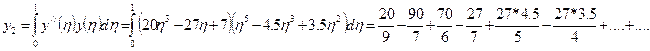в результате вычисления определенных интегралов получаются амплитуды прогибов А.

После этого необходимо посмотреть следующие эпюры:

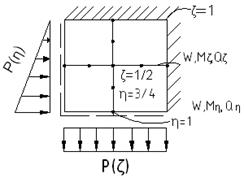
Чтобы не ошибиться, можно использовать ПЭВМ;

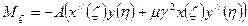
Можно записать:

WRITE (‘x=’); READLN (x);

WRITE (‘y=’); READLN (y);

WRITE (‘A=’); READLN (A);

MKS:=-A*((12*x*x-9*x)*(y*y*y+y*…)+MU*…)

WRITELN(‘MKS=’,MKS);