Лекция 31
Расчет пластинок методом Власова-Конторовича
Рассмотрим конкретную пластинку.
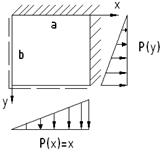
Входные данные: a, b, h, E, μ.
Условие закрепления пластинки (4)
Условие нагружения q(x,y) – аналогичная функция.
Если распределение q(x,y) сложное, то нагрузку следует разложить в ряд и получить решение на каждый член ряда. Затем полученное суммируется.
Расчет загружения половины плоскости. По нормам расчет ведется по загружению всей половины и четверти плоскости.

Удобнее решать задачу в безразмерном виде.
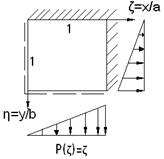
Входными параметрами являются:
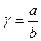
Условие закрепления (4)
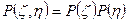 - функция с разделяющимися переменными
- функция с разделяющимися переменными
При этом необходимо записать в безразмерном виде дифференциальные уравнения изгиба пластин:
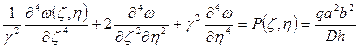 (1)
(1)
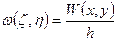
Необходимо записать граничные условия:
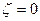 :
: 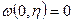 ,
, 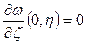 - жесткое закрепление
- жесткое закрепление
Если шарнирное закрепление:
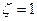 :
: 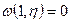 ,
, 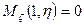
Т.к. сторона шарнирного закрепления 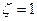 остается прямой, то =>
остается прямой, то => 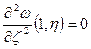 (2)
(2)
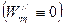
Шарнирное закрепление 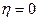 :
: 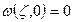 ,
,  =>
=> 
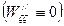
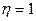 :
: 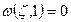 ,
, 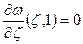
В соответствии с методом Власова-Канторовича запишем:
 (3)
(3)
Одну из функций необходимо построить по методу В.З. Власова.
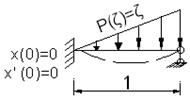
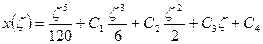
С3=0, С4=0
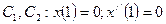
После этого функция 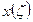 становится полностью определенной.
становится полностью определенной.
Используем принцип Лагранжа.
Сумма работ внешних и внутренних сил упругости системы на любом возможном и бесконечно молом равно 0.
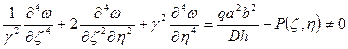 :
: 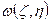 заменено приближенным выражением.
заменено приближенным выражением.
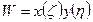 - приближенное выражение.
- приближенное выражение.
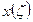 - известная функция
- известная функция
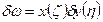
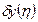 - малое возмущение
- малое возмущение
Тогда получим:
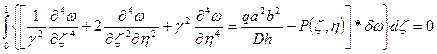
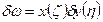
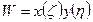
Все величины, зависящие от η, могли быть получены из-под значения интеграла:
 (4)
(4)
Т.к. функция 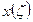 известна, то известны и величины определенных интегралов:
известна, то известны и величины определенных интегралов:
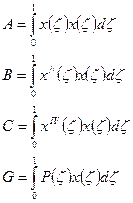
В результате из выражения (4) получается обыкновенное дифференциальное уравнение вида, дающая точное решение.
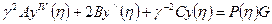 (5)
(5)
Если рассмотреть полное дифференциальное обыкновенное уравнение с переменными коэффициентами, то для решения можно использовать метод конечных разностей.
Т.к. (5) является неоднородным уравнением, то решение запишется в виде:
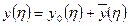 - решение неоднородного уравнения, определяемое правилом (5) (6)
- решение неоднородного уравнения, определяемое правилом (5) (6)
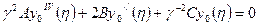 (7)
(7)

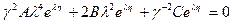
Приходим к алгебраическому уравнению (характеристическому):
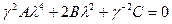 (8)
(8)
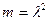
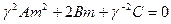
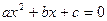
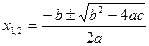 ,
, 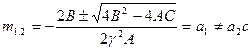
Решение получается в комплексном виде. Необходимо преобразовать его в вид:
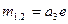
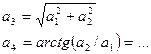
Тогда нужно подсчитать 2 величины:
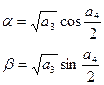
Тогда решение однородного уравнения запишется в виде:
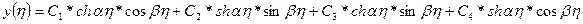
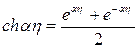
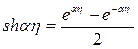
После этого необходимо частное найти решение уравнения: 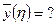
Т.к. нагрузка по оси η постоянна и 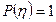 , то
, то 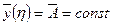
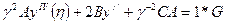
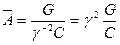 - число
- число
Тогда общее решение: 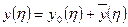
Если реализуется случай Р(η)=η, то 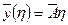
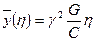
Остается найти произвольную постоянную интегрирования из условия закрепления пластинки по оси η
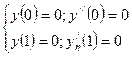
Получается система 4-х алгебраических уравнений относительно С1, С2, С3, С4, из которых находим эти величины.
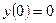 :
: 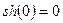 ,
, 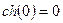
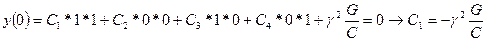
Записываем выражение для производной функции у(η)
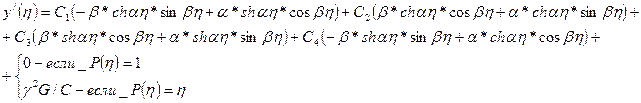
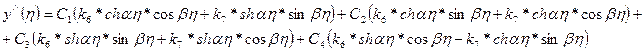
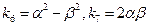
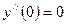 ,
, 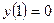 ,
, 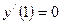 ,
, 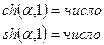 ,
, 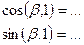
Дата добавления: 2015-08-01; просмотров: 765;
