Лекция 28

Построение аппроксимирующих функций статическим методом В.З.Власова

Аналогично поступаем по другому направлению:

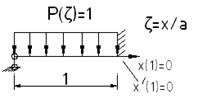
Записываем дифференциальное уравнение изгиба балки, вырезанной из пластинки:

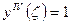(1)

Граничные условия: х(0)=0, х^II(0)=0

Получаем выражение для х(ζ):

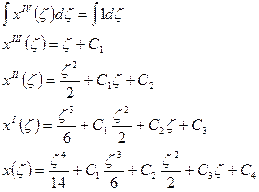
Используем граничные условия для нахождения произвольных постоянных интегрирования:

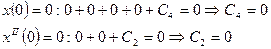
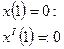
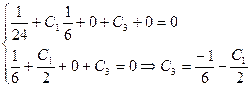
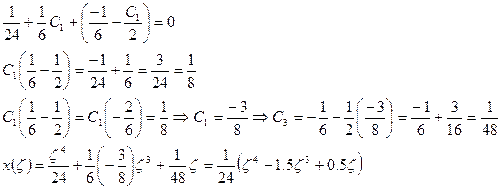
Принимаем для дальнейших расчетов:

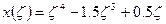
Проверяем, удовлетворяет ли функция граничным условиям:

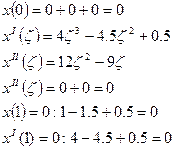
Таким же образом можно проверить функцию у(η):

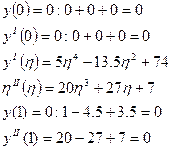
Надо помнить, что старшая степень х(ζ)=4, т.к. нагрузка ζ и η поставлена. В у(η) старшая степень 5, т.к. нагрузка изменяется линейно.

Рассмотрим пластинку со свободным закреплением края:

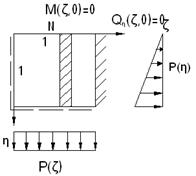
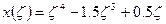
Вырезаем из пластинки полоску по направлению оси η. Рассматриваем балку.

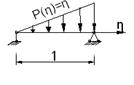
Записываем дифференциальное уравнение изгиба балки:

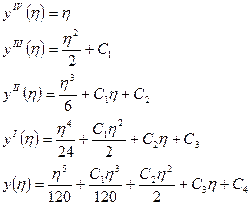
На свободном крае:

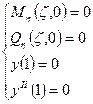
Рассмотрим выражение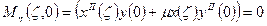

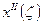и 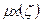меняется вдоль свободной стороны 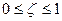, т.е. результат будет разный, если взять ζ=ζ₁, ζ=ζ₂, ….

Записываем функцию прогиба в виде: 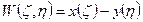- запись с разделяющимися переменными, при этом в решении выносится некоторая погрешность.

Производим смягчение граничащих условий по принципу Сен Венона:

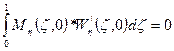- сумма работ изгибающих моментов на углах поворота вдоль стороны η равно 0. Данная запись следует из вариационной формулировки задачи.

Очевидно, что запись примет вид:

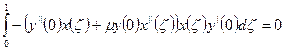
Интегрирование идет по ζ, поэтому величины, зависящие от η можно вынести за знак интеграла:

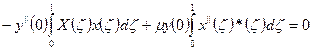
В данном случае у нас X(ζ)- известная функция: 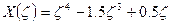, поэтому величины определенных интегралов могут быть подсчитаны:

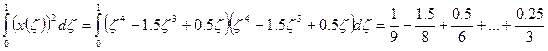
Известно, что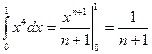

В EXCEL подсчет определенных интегралов:

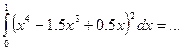
В результате в полученной нами записи оказывается: обозначим

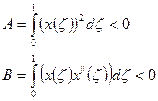
В результате получаем уравнения:

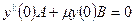
Подставляя сюда выражения для 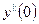и :

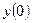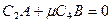(1)

Аналогично поступаем со вторым граничным условием:

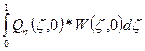- сумма поперечных сил Кирхгофа на прогибы 0

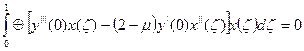
В результате некоторых преобразований получаем:

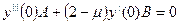
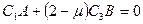(2)

Дописываем (3) и (4) уравнения в данную систему:

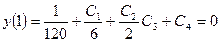(3)

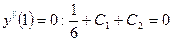(4)

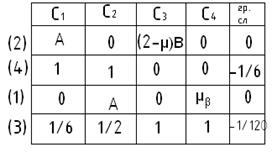
Получаем систему четырех уравнений с четырьмя неизвестными.

На главной диагонали должны стоять не нулевые коэффициенты: