Классификация граничных условий
 Граничные условия бывают:
Граничные условия бывают:
Геометрическими, статическими и смешанными.
 – геометр. гр. усл.
– геометр. гр. усл.
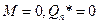 – статич. гр. усл.
– статич. гр. усл.
Граничные условия подразделяют на однородные и неоднородные .
Схема подхода к решению задач прочности пластины.
1. Анализ конструкции
2. Расчётная схема
3. Математическая модель
4. Численная реализация матем. модели
Построение аппроксимирующих функций статическим методом В.З.Власова
В.З.Власов (1906-1958гг) предложил способ построения функций распределения прогиба пластины, удовлетворяющих как граничным условиям, так и характеру распределения внешней нагрузки.
К входным параметрам относятся: a, b, h (м)-(1,2,3), толщина пластины; E(Па), μ(безр)- (4,5), условие закрепления (6,7,8,9); q(x,y) (10) (при расчете в размерном виде)
Σ10
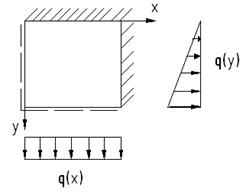
При решении в безразмерном виде решению соответствует бесконечное множество пластин для любых значений а(м), h(м), Е(Па)
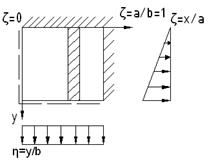
Далее рассчитываем пластинку в безразмерном виде:
По алгоритму статического метода В.З.Власова необходимо:
1.Вырезаем из пластинки полоску по одному направлению
2.Рассматриваем данную полоску как обыкновенную балку

Дифференциальное уравнение изгиба балки имеет вид:
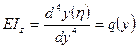
В безразмерном виде: 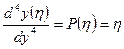 (1)
(1)
Кроме того используются граничные условия:
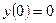 ;
; 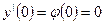
Необходимо получить выражение y(η) и для ее производной.
Интегрируем выражение (1): 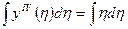 ;
; 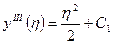 ;
;
 =>
=> 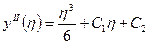 ;
; 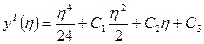 ;
;
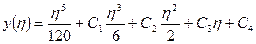
Используем граничные условия для нахождения С1, С2, С3, С4:
y(0)=0: 0+0+0+0+С4 =0 => С4=0
yI(0)=0: 0+0+0+C3=0 => C3=0
Используем граничные условия на правом конце балки для подсчета величин С1 и С2:
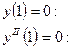
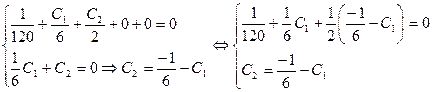
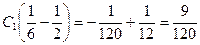 ;
; 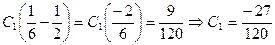
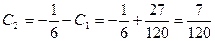
Подставляя полученные значения:
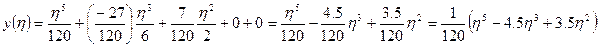
- точное решение для балки, но приближенное решение для пластинки, по направлению у.
Амплитуда прогиба пластинки не связана с амплитудой прогиба балки и затем будет найдена из решения задачи по одному из методов
В проведенный характер изменения прогиба пластинки по направлению оси η.
Т.е. для дальнейших расчетов применим:
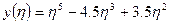
Дата добавления: 2015-08-01; просмотров: 1266;
