Неподвижной оси

Найдем условия отсутствия ударных реактивных импульсов.

Для этого в первых пяти уравнениях (8.22) положим их равными нулю. Тогда уравнения (8.22) примут вид:

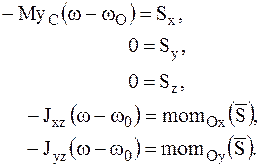(8.23)

Из второго и третьего уравнений (8.23) следует, что для отсутствия ударных реактивных импульсов необходимо, чтобы приложенный ударный импульс был направлен параллельно оси Оx, то есть перпендикулярно плоскости yОz, которая проходит через ось вращения и центр масс АТТ (рис. 53).

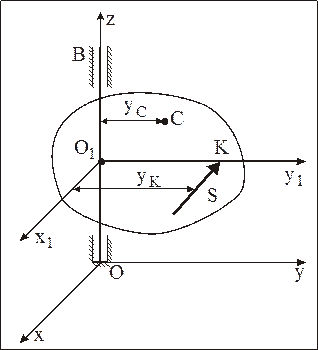
Рис. 53

Так как систему координат можно выбрать произвольно, то выберем ее такой, чтобы ударный импульс 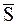лежал в координатной плоскости x₁O₁y₁ (точка О₁ расположена на оси вращения z). Тогда, направив 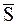согласно условиям 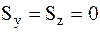параллельно оси O₁x₁, получим:

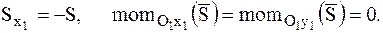
В результате четвертое и пятое из уравнений (8.23) дадут следующие условия:

,

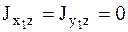то есть ось вращения z для точки О₁ должна быть главной осью инерции.

Следовательно, для отсутствия ударных реактивных импульсов необходимо расположить ударный импульс 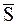в плоскости x₁O₁y₁, проходящей через точку О₁, для которой ось z является главной осью инерции.

Первое соотношение (8.23) примет вид:

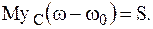(8.24)

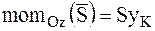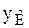Так как в рассматриваемом случае , где – кратчайшее расстояние линии действия ударного импульса 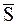от оси вращения z, то шестое соотношение формулы (8.22) примет вид:

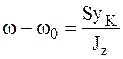. (8.25)

Из уравнений (8.24) и (8.25) найдем после исключения разности 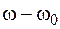следующее соотношение:

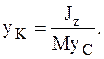(8.26)

Таким образом, уравнение (8.24) будет иметь место при любой численной величине ударного импульса 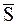, если линия действия этого импульса будет проходить через точку К, которая отстоит от оси вращения z на расстоянии y_К, определяемом формулой (8.26).

Условиями отсутствия ударных реактивных импульсов АТТ, вращающегося вокруг неподвижной оси, являются:

ударный импульс должен быть перпендикулярен плоскости, проходящей через ось вращения z и центр масс АТТ;

ударный импульс должен быть расположен в плоскости, перпендикулярной оси z и проходящей через точку О₁ АТТ, для которой ось z является главной осью инерции;

точка приложения К ударного импульса должна находиться от оси z на расстоянии, определяемом формулой (8.26) (точку К, через которую при этом проходит линия действия ударного импульса, не вызывающего ударных реакций в точках закрепления оси, называют центром удара).

В частном случае, если центр масс АТТ находится на оси вращения, т. е. 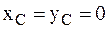, то из формулы (8.26) следует 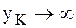. То есть в этом случае нельзя добиться отсутствия ударных реактивных импульсов. Так как дополнительные динамические реакции АТТ, вращающегося вокруг неподвижной оси (глава 5) , могут отсутствовать только в случае, если ось вращения является центральной ( 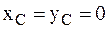), то добиться одновременно отсутствия дополнительных динамических реакций и ударных реактивных импульсов АТТ, вращающегося вокруг неподвижной оси при ударе, невозможно.

Заключение

Алгоритм динамики – управляющий