Прямой удар МТ о неподвижную поверхность
Определение: Прямым ударом МТ о неподвижную поверхность называют такой удар, при котором скорость МТ в начале удара направлена по нормали к поверхности в момент ее соприкосновения с МТ.
Рассмотрим прямой удар свободно падающей МТ массы m о неподвижную горизонтальную плоскость или о поверхность, нормаль к которой в точке удара вертикальна (рис. 49).
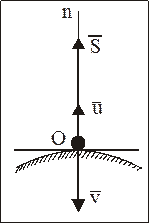
Рис. 49
При таком ударе скорости МТ в начале и после удара направлены по нормали к поверхности в точке удара. Обозначим импульс этой ударной силы через 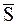 . Действием же при ударе неударной силы (силы тяжести) пренебрегаем. Тогда, используя основное уравнение теории удара (8.1), можно записать:
. Действием же при ударе неударной силы (силы тяжести) пренебрегаем. Тогда, используя основное уравнение теории удара (8.1), можно записать:
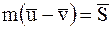 .
.
Проектируя обе части этого равенства на внешнюю нормаль On в точке удара, получим:
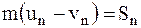 .
.
При прямом ударе 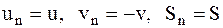 , поэтому
, поэтому
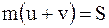 . (8.3)
. (8.3)
Если скорость МТ в начале удара известна, то в уравнении (8.3) будут две неизвестные величины u и S. Очевидно, что для решения задачи необходимо получить дополнительную зависимость между входящими в уравнение (8.3) величинами.
Характер явления удара заставляет отступить от гипотезы абсолютно твердого тела и учитывать деформацию поверхности.
Различаются две фазы удара. В течение первой фазы поверхность деформируется (сжимается) до тех пор, пока скорость МТ не станет равной нулю; при этом происходит переход кинетической энергии МТ во внутреннюю потенциальную энергию поверхности. В течение второй фазы удара форма поверхности под действием внутренних сил упругости частично восстанавливается. За эту вторую фазу скорость МТ возрастает до определенной конечной величины. Одновременно происходит переход внутренней потенциальной энергии поверхности в кинетическую энергию МТ. В тот момент, когда МТ отделится от поверхности, явление удара заканчивается. Во второй фазе удара восстанавливается только часть первоначальной кинетической энергии, а другая преобразуется в деформацию поверхности и ее нагревание.
Таким образом, скорость МТ в конце удара будет составлять какую-то часть скорости в начале удара и может быть определена равенством:
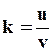 . (8.4)
. (8.4)
Отношение модулей скоростей шара после и до удара называется коэффициентом восстановления k при ударе.
Значение k для разных тел определяется опытным путем. Опыты показывают, что для различных тел k различно и изменяется от нуля до единицы (0 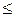 k
k 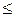 1).
1).
Удар, при котором имеет место зависимость (8.4) при 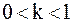 , называют не вполне упругим ударом.
, называют не вполне упругим ударом.
Из уравнений (8.3) и (8.4), зная m, v , k, найдем неизвестные величины u, S:
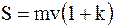 ,
,
u = kv.
Если k = 0, то такой удар называют абсолютно неупругим, и в этом случае явление удара заканчивается одной первой фазой. Так как в этом случае u=0, то при абсолютно неупругом ударе МТ, ударившись о неподвижную поверхность, остается неподвижной, при этом
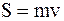 .
.
Если же k = 1, то такой удар называют абсолютно упругим. В этом случае u = v, то есть скорость МТ в конце удара равна по модулю ее скорости в начале удара. При этом
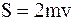 .
.
Дата добавления: 2015-08-01; просмотров: 691;
