Косой удар МТ о неподвижную поверхность

Определение: Косым ударом МТ массы m об абсолютно гладкую неподвижную поверхность, называется такой удар, при котором скорость 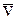МТ в начале удара образует с нормалью Оn к поверхности в точке удара какой-либо угол.

Пусть угол a – угол падения, а скорость 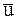в конце удара направлена к этой нормали под некоторым углом b – угол отражения (рис. 50).

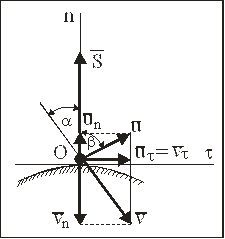
Рис. 50

В рассматриваемом случае действующей на МТ ударной силой, как в случае прямого удара, будет нормальная реакция поверхности. Обозначим импульс этой ударной силы через .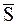

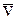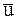Проектируя обе части уравнения (8.1) на нормаль к поверхности в точке удара и касательную, проведенную в плоскости векторов и , получим

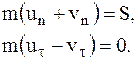(8.5)

Из последнего равенства следует, что

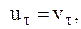
т. е. касательная составляющая скорости МТ при ударе об идеальную гладкую поверхность не изменяется.

Так как влиянием трения пренебрегаем и, следовательно, удар происходит только по направлению нормали к поверхности в точке удара, то аналогично соотношению (8.4), запишем

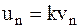. (8.6)

В результате из соотношений (8.5) и (8.6) можно найти модуль и направление скорости МТ в конце удара и ударный импульс, если m, v и k известны:

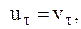
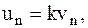
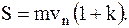(8.7)

На рис. 50 видно, что

.

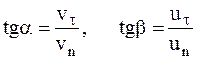Поделив эти соотношения почленно и учтя, что 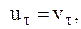находим

,

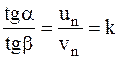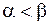т. е. в случае косого удара коэффициент восстановления есть отношение тангенса угла падения к тангенсу угла отражения. При не вполне упругом ударе , и, следовательно, , т. е. угол падения меньше угла отражения.

В частном случае абсолютно упругого удара 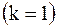будем иметь 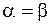, то есть угол падения равен углу отражения, а при абсолютно неупругом ударе .

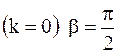8.4. Теорема об изменении количества

движения СМТ при ударе

Рассмотрим СМТ, состоящую из n МТ, и выделим n-ю МТ с массой .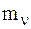

Так же как при доказательстве общих теорем динамики СМТ, разделим все ударные импульсы, действующие на МТ, на внешние и внутренние. Тогда основное уравнение теории удара (8.1) для n-й МТ рассматриваемой СМТ примет вид:

,

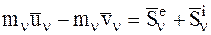где 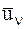и 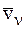– скорости n-й МТ соответственно в конце удара и в начале удара, – равнодействующая всех внешних ударных импульсов, приложенных к n-й МТ, а 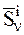– равнодействующая всех внутренних ударных импульсов, приложенных к той же МТ.

Составив такие уравнения для всех n МТ рассматриваемой СМТ и сложив их почленно, получим:

.

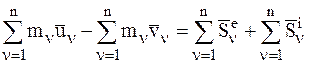Введя следующие обозначения: 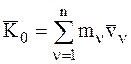– количество движения СМТ до удара, 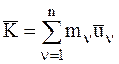– количество движения СМТ после удара и учтя, что 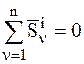, так как внутренние ударные импульсы на основании третьего закона динамики - закона равенства действия и противодействия попарно равны по модулю и противоположны по направлению, получим:

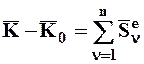. (8.8)

Теорема: Изменение количества движения СМТ за время удара равно геометрической сумме всех внешних ударных импульсов, действующих на эту СМТ.

Проектируя соотношение (8.8) на координатные оси, получим скалярную форму теоремы об изменении количества движения СМТ при ударе:

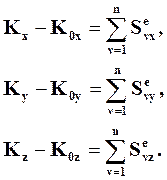(8.9)

Из соотношений (8.9) следует, что изменение проекции количества движения СМТ на какую-либо ось за время удара равно сумме проекций всех ударных импульсов внешних ударных сил, действующих на СМТ, на ту же ось.

Используя соотношения (8.8) и (8.9), можно получить два следствия, аналогичных двум следствиям, полученным для этой теоремы в главе 4.