Вращение вокруг неподвижной оси

Найдем сначала выражение для момента импульса твердого тела относительно оси вращения OO' (рис.1.9.1). Воспользовав­шись формулами (1.5.9) и (1.5.10), запишем

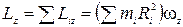
где m_i и R_i — масса и расстояние от оси вращения i-й частицы твердого тела, w_z — его угловая скорость. Обозначив величину, стоящую в круглых скобках, через I, получим Рис.1.9.1.

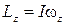(1.9.2) где I — момент инерции твердого тела относительно оси ОО':

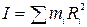(1.9.3)

Момент инерции твердого тела зависит, как нетрудно видеть, от распределения масс относительно интересующей нас оси и является величиной аддитивной.

При непрерывном распределении массы по некоторому объему вычисление момента инерции тела проводится по формуле

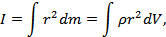(1.9.4)

где dm и dV — масса и объем элемента тела, находящегося на расстоянии r от интересующей нас оси Z; r — плотность тела в данной точке.

Вычисление момента инерции твердого тела произвольной формы относительно той или иной оси представляет собой, вооб­ще говоря, довольно кропотливую в математическом отношении задачу. Однако в некоторых случаях нахождение момента инер­ции значительно упрощается. Обычно для симметричных тел рассчитать момент инерции относительно оси, проходящей через центр масс, оказывается несложно. Тогда достаточно легко найти момент инерции относительно произвольной оси, если воспользоваться теоремой Штейнера: момент инерции I относительно произвольной оси Z равен моменту инерции I_С относительно оси Z, параллельнойданной и проходящей через центр масс C тела, плюс произведение массы m тела на квадрат расстояния l между осями:

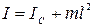. (1.9.5)

Таким образом, если известен момент инерции I_С, то нахождение момента инерции I элементарно.

Приведем пример расчета момента инерции. Найдем момент инерции однородного параллелепипеда относительно оси, проходящей через одно из его ребер О. Для этого сначала определим момент инерции относительно оси, проходящей через центр масс С, который в данном случае является центром симметрии. Длины ребер параллелепипеда равны а, b, с, плотность материала параллелепипеда 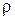. Выберем в параллелепипеде бесконечно малый объем 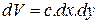, расположенный на расстоянии r от оси С. Масса этого элемента dm= 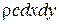. Тогда момент инерции относительно оси С равен

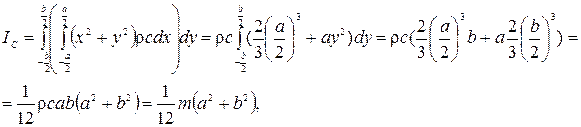
а момент инерции относительнооси О

.

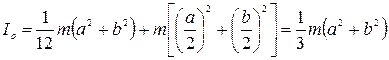Если b» a и b» c (тело будет представлять собой стержень), то

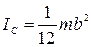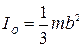, . (1.9.6)

Уравнение динамики вращения твердого тела

(ось враще­ния неподвижна). Это уравнение легко получить как следствие (1.5.7), если продифференцировать (1.9.2) по времени, тогда

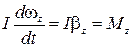, (1.9.7)

где М_z — суммарный момент всех внешних сил относительно оси вращения. Из этого уравнения, в частности, видно, что мо­мент инерции I определяет инерционные свойства твердого тела при вращении: при одном и том же значении момента сил М_z тело с большим моментом инерции приобретает меньшее уг­ловое ускорение b_z. Уравнение (1.9.7) называют основным уравнением динамики вращения твердого тела относительно оси.

Напомним, что моменты сил относительно оси — величины алгебраические: их знаки зависят как от выбора положительного направления оси Z (совпадающей с осью вращения), так и от направления «враще­ния» соответствующего момента силы. Например, выбрав положительное направление оси Z (рис.1.9.3), мы задаем и положительное направле­ние отсчета угла j (оба эти направления связаны правилом правого винта). Если некоторыймоментМ_iz Рис.1.9.3.

«враща­ет» в положительном направлении угла j, то этот

момент счи­тается положительным, и наоборот. А знак суммарного момен­та М_z в свою очередь определяет знак b_z — проекции вектора углового ускорения на ось Z.

Интегрирование уравнения (1.9.7) с учетом начальных усло­вий — значений w_0z и j₀ в начальный момент времени — по­зволяет полностью решить задачу о вращении твердого тела во­круг неподвижной оси, т. е. найти зависимость от времени уг­ловой скорости и угла поворота, w_z(t) и j(t).

Заметим, что уравнение (1.9.7) справедливо в любой системе отсчета, жестко связанной с осью вращения.

Кинетическая энергия вращающегося твердого тела

Имея в виду, что скорость i-й частицы вращающегося твердого тела 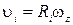,запишем

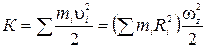
или, короче,

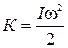(1.9.8)

где I — момент инерции тела относительно оси вращения, 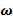— его угловая скорость. Если ось проходит через центр масс, то получим выражение для собственной энергии

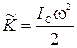. (1.9.9)

Работа внешних сил при вращении твердого тела вокруг неподвижной оси.

В соответствии с уравнением (1.6.10) работа всех внешних сил, действующих на твердое тело, равна прираще­нию только кинетической энергии тела, так как его собствен­ная потенциальная энергия при этом не меняется. Таким образом, δA=dK или, согласно (1.9.8),δA = d(Iw²/2). Так как осьZ совпадает с осьювращения, то 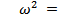и

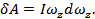
Но согласно (1.9.7), 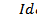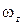= М_zdt. Подставляя это выражение в последнееуравнение дляδAи, учитывая, что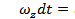 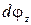, получаем

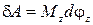(1.9.10)

РаботаδA — величина алгебраическая: еслиМ_z и 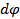имеют одинаковыезнаки, тоδA > 0; если же их знаки противоположны, тоδA < 0.

Работа внешних сил при повороте твердого тела на конечный угол равна

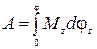. (1.9.11)

В случае еслиМ_z = const, выражение (1.9.11) упрощается: А = М_z .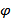

Таким образом, работа внешних сил при вращении твердого тела вокруг неподвижной оси определяется действием момента этих сил относительно данной оси. Если силы таковы, что их момент М_z = 0, то работы они не производят.