Потенциальная энергия и сила поля

Взаимодействие частицы с окружающими телами можно описывать двумя способами: с помощью сил или с помощью потенциальной энергии. В ньютоновской механике оба способа используют одинаково широко. Однако первый способ обладает несколько большей общностью, так как он применим и к таким силам, для которых нельзя ввести потенциальную энергию (например, к силам трения). Второй способ применим только в случае консервативных сил.

Наша задача — установить связь между потенциальной энергией и силой поля. Мы уже знаем, что при перемещении частицы из одной точ­ки стационарного поля консервативных сил в другую работа, которую производят силы поля, может быть представлена как убыль потенциальной энергии частицы в поле, т. е. при элементарном перемещении dl,

δА = -dU, (1.7.1)

или

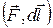= - dU. (1.7.2)

Имея в виду, что 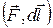= F dl, где dl — элементарный путь, F — проекция вектора силы на перемещение, перепишем уравнение (1.7.2) в форме

F 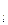dl = - dU,

где -dU — убыль потенциальной энергии в направлении перемещения. Отсюда

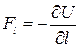(1.7.3)

т. е. проекция силы поля в данной точке на направление перемещения равна с обратным знаком производной потенциальной энергии U по данному направлению. Сим­вол ∂/∂l — частной производной — подчеркивает, что производная берется по определенному направлению.

Перемещение можно взять в любом направлении, в частности вдоль координатных осей X, Y, Z. Если перемещение, например, параллельно оси X, то его можно представить так: 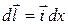, где 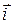— орт оси X, dx — приращение координаты х. Тогда работа силы на перемещении , параллельном оси X,

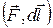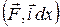= = F_xdx,

где F 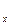— проекция вектора 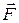на орт 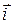. Подставив последнее выражение в уравнение (1.7.3), получим

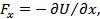
где символ частной производной означает, что U(x, у, z) при дифференцировании должна рассматриваться как функция од­ного аргумента х, остальные же аргументы должны оставаться при этом постоянными. Ясно, что для проекций F_y и F_z уравнения будут аналогичны уравнению для F_x.

Итак, взяв с обратными знаками частные производные функции U по х, у и z,мы найдем проекции F_x, F_y и F_z вектора F на орты 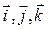. Отсюда легко найти и сам вектор: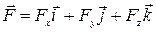

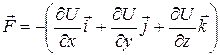. (1.7.4)

Величину, стоящую в скобках, называют градиентом скалярной функции U,

т. е. сила поля равна со знаком минус градиенту потенциальной энергии частицы в данной точке поля.

Механическая энергия частицы и системы частиц.

Движущаяся частица, на которую действуют консервативные силы, обладает кинетической и потенциальной энергией. Сумма кинетической и потенциальной энергии частицы называется ее механической энергией

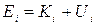. (1.7.5)

Кинетическую энергию системы частиц можно рассчитать по формуле (1.6.11). Потенциальная энергия, так же как и кинетическая, является величиной аддитивной, т.е. находится суммированием энергий отдельных частиц. Поэтому механическая энергия системы

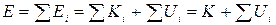. (1.7.6)

Консервативные силы, действующие на систему частиц можно разделить на внутренние и силы 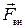со стороны внешних потенциальных полей 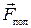. В соответствии с этим потенциальную энергию системы делят на энергию, обусловленную внутренними силами ( 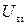) и энергию во внешних полях ( 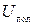). Тогда потенциальная энергия системы и полной механической энергией системы частиц будем называть

. (1.7.7)

Закон сохранения механической энергии.

Поскольку изменение кинетической энергии системы (как и для одной частицы) равно работе всех сил, ее можно разделить на работу консервативных и неконсервативных сил

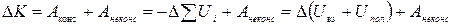, (1.7.8.) где 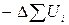- убыль потенциальной энергии системы, что следует из (1.7.1). Из (1.7.7) и (1.7.8) следует

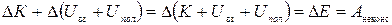. (1.7.9)

Из уравнения (1.7.9) вытекает закон сохранения полной ме­ханической энергии системы, находящейся во внешнем стаци­онарном поле консервативных сил: если на систему частиц не действуют внешние и внутренние дисси­пативные силы, то полная механическая энергия системы остается постоянной

(1.7.10)

Если система тел не находится во внешнем потенциальном поле, то ее механическую энергию 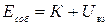называют собственной механической энергией. Для такой системы, если она замкнута и в ней отсутствуют внутренние диссипативные силы, собственная механическая энергия сохраняется в процессе движения

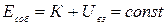(1.7.11)

Такую систему называют консервативной. Тогда можно сформулировать закон сохранения механической энергии: механическая энергия консервативной системы не меняется с течением времени.При движении замкнутой консервативной системы сохраняется именно меха­ническая энергия Е_со6,кинетическая же и потенциальная в об­щем случае изменяются. Однако эти изменения происходят всегда так, что приращение одной из них в точности равно убыли другой.Это положение справедливо только в инерциальных системах отсчета.

Из уравнения (1.7.9) следует, что если замкнутая система не консервативна, т.е. в ней имеются диссипативные силы, то механическая энергия такой систем убывает (работа внутренних диссипативных сил отрицательна).Уменьшение механической энергии обусловлено тем, что она расходуется на работу против диссипативных сил, действующих в системе. Однако такое объяснение является формаль­ным, поскольку оно не раскрывает физической природы диссипативных сил.

Более глубокое осмысливание этого вопроса привело к фундаментальному выводу о существовании в природе универсального закона сохранения энергии: энергия никогда не создается и не уничтожается, она может только переходить из одной формы в другую или обмениваться между отдельными частями материи. При этом понятие энергии пришлось расширить введением понятий о новых формах ее (помимо механиче­ской) — энергия электромагнитного поля, химическая энер­гия, ядерная и др.

Универсальный закон сохранения энергии охватывает, таким образом, и те физические явления, на которые законы Ньютона не распространяются. Поэтому он не может быть выведен из этих законов, а должен рассматриваться как самостоятельный закон, представляющий собой одно из наиболее широ­ких обобщений опытных фактов.

При уменьшении механической энергии замкнутой системы всегда возникает эквивалентное количество энергии других ви­дов, не связанных с видимым движением. В этом смысле уравнение (1.7.9) можно рассматривать как более общую формулировку закона сохранения энергии, в которой указана причина изменения механической энергии системы.

В частности, механическая энергия может сохраняться у незамкнутых систем, но это происходит лишь в тех случаях, когда, согласно уравнению (1.7.9), уменьшение этой энергии за счет работы против внутренних диссипативных сил компенси­руется поступлением энергии за счет работы внешних сил.

Внутренняя энергия системы частиц. Устойчивость системы.

Механическую энергию системы частиц можно записать

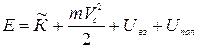. (1.7.12) Сумму собственной кинетической энергии 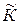(энергия в системе центра инерции) и потенциальной энергии взаимодействия между частицами системы 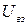называют внутренней энергией системы

. (1.7.13)

Тогда энергия системы 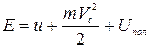. (1.7.14)

Сформулируем условие устойчивости системы частиц, т.е. условие, при котором она будет существовать как целое, не распадаясь на составляющие. Пусть система состоит из двух подсистем. Тогда в Ц-системе механическую энергию системы частиц можно записать

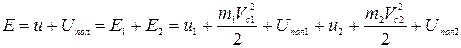, (1.7.15) где цифрами 1 и 2 обозначены части энергии каждой подсистемы.

Для простоты положим, что внешние поля отсутствуют 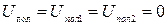. Тогда из (1.7.15) следует

. (1.7.16)

Если 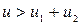, то часть внутренней энергии системы может перейти в кинетическую энергию подсистем и система распадется на составляющие подсистемы. Таким образом, чтобы система была устойчивой, нужно, чтобы внутренняя энергия системы была меньше суммы внутренних энергий ее частей 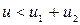. (1.7.17)

Это условие подтверждается на примере атомного ядра, у которого энергия меньше суммы энергий частиц, из которых оно состоит.

Лекция 1.8.

Условие равновесия тел. Столкновения.

Условия равновесия механической системы. Потенциальный барьер. Потенциальная яма.

Рассмотрим материальную точку, которая может совершать одномерное движение вдоль некоторого направления, которое обозначим х. Частица находится в потенциальном поле. Зависимость потенциальной энергии частицы от координаты х приведена на рис.1.8.1. Неконсервативные силы на частицу не действуют. Поэтому механическая энергия частицы остается постоянной.

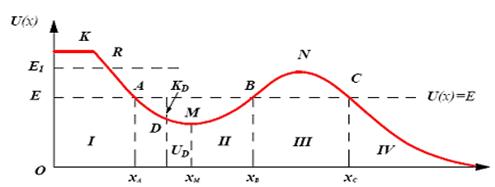
Рис.1.8.1.

Из (1.7.10) следует, что кинетическая энергия может возрастать только за счет уменьшения потенциальной. Поэтому, если частица находится в таком состоянии, что ее скорость равна нулю, а потенциальная энергия имеет минимальное значение, то без воздействия извне она не сможет прийти в движение, т.е. будет находиться в равновесии. В положении равновесия ускорение частицы равно нулю, следовательно, равна нулю сила, действующая на нее.

Из (1.7.3) следует, что 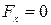, если 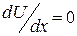, что соответствует максимуму или минимуму потенциальной энергии. На графике рис 1.8.1 этому условию удовлетворяют точк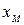и и 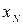. Однако, условия для частицы в этих точках различны. Если сместить частицу из положения 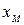, например, в положение , то, как видно из графика, в этой точке 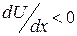, а, следовательно, как видно из (1.7.10), 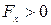. Таким образом, эта сила вернет частицу в положение равновесия. Это положение устойчивого равновесия. Если же проделать то же самое, сместив частицу из положения 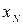, то возникшая сила уведет частицу еще дальше от положения равновесия. Это положение неустойчивого равновесия. Резюмируя все сказанное, заметим: любая система стремится к состоянию с минимальной потенциальной энергией.

Зная вид функции потенциальной энергии, можно сделать ряд заключений о характере движения частицы. Если полная механическая энергия имеет значение Е, указанное на рис.1.8.1, то, поскольку полная энергия не может быть меньше потенциальной, то частица может совершать движение либо в пределах от 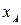до 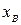, либо от 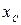до бесконечности. В области 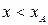(область Ι) и 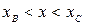(область ΙΙΙ) частица с энергией Е проникнуть не может, так как в этой области потенциальная энергия больше Е (если бы это случилось, то кинетическая энергия стала бы отрицательной). Таким образом, область 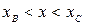представляет собой потенциальный барьер, через который частица не может проникнуть, имея данный запас энергии. Область 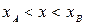(область ΙΙ) называется потенциальной ямой.

Столкновения.

Столкновением называется любое кратковременное взаимодействие, когда время взаимодействия много меньше полного времени их движения. Поэтому для столкновений можно с большой степенью точности считать справедливым закон сохранения импульса. Частным случаем столкновений является механическое соударение тел. В дальнейшем мы будем говорить о столкновении частиц (материальных точек). Однако полученные выводы относятся и к другим телам, если в уравнения будут входить скорости их центров масс. Обычно рассматривают столкновение двух частиц.

Все столкновения можно разделить на лобовые и нелобовые. При лобовых столкновениях начальные импульсы тел направлены вдоль линии, проходящей через их центры масс. В этом случае после соударения тела либо будут двигаться в том же направлении либо изменить направление движения на противоположное. Все другие – являются нелобовыми.

Для системы сталкивающихся тел справедлив закон сохранения полной энергии. Из (1.7.14) следует ,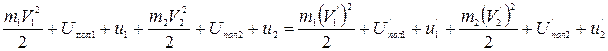

(1.8.1)

где штрихами обозначены величины после соударения. За краткое время соударения положение тел во внешних полях практически не изменится. Поэтому потенциальная энергия тел до и после соударения остается неизменной. Тогда (1.8.1) перепишется

. (1.8.2)

В дальнейшем рассмотрим только лобовые соударения.

В зависимости от свойств соударяющихся тел все столкновения можно разделить на упругие и неупругие.

Упругие лобовые столкновения.

Упругим называется столкновение, в результате которого внутренняя энергия тел не изменяется. Тогда из (1.8.2) следует, что в таком случае сохраняется суммарная кинетическая энергия тел до и после столкновения. Для нахождения скоростей тел после соударения записывают закон сохранения кинетической энергии и закон сохранения импульса

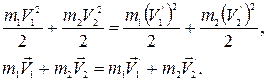(1.8.3)

Решая эту систему, получим скорости тел после соударения:

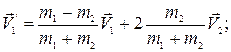
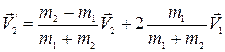. (1.8.4)

Рассмотрим частные случаи

1. Массы соударяющихся тел одинаковы. Тогда 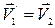, , 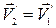т.е. тела в результате соударения обмениваются скоростями.

2. Масса одного тела много больше массы другого 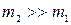. В этом случае

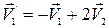; . В частности, если скорость второго тела до столкновения равна нулю, то 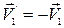; =0, т.е. второе тело практически не меняет своей скорости (остается неподвижным), а первое – отскакивает в противоположную сторону с неизменной по величине скоростью.

Абсолютно неупругие соударения.

Для решения задачи о неупругом соударении нужно решить совместно уравнение закона сохранения импульса и уравнение (1.8.2), т.е. нужно знать какая доля кинетической энергии переходит во внутреннюю.

Частным случаем неупругого столкновения является абсолютно неупругое соударение. В этом случае тела после взаимодействия движутся как единое целое с одной и той же скоростью. Для нахождения скорости тел после соударения достаточно одного закона сохранения импульса .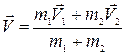

Лекция 1.9.

Динамика абсолютно твердого тела.

Движение твердого тела в общем случае определяется двумя векторными уравнениями. Одно из них — уравнение движения центра масс (1.4.8), другое — уравнение моментов в Ц-системе (1.5.11):

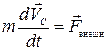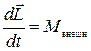; .(1.9.1)

Зная действующие внешние силы, точки их приложения и начальные условия, можно с помощью этих уравнений найти как скорость, так и положение каждой точки твердого тела в любой момент времени, т. е. полностью решить задачу о движении тела. Однако, несмотря на кажущуюся простоту уравнений (1.9.1), решение их в общем случае представляет собой весьма трудную задачу. И прежде всего это обусловлено тем обстоятельством, что связь между собственным моментом импульса и скоростями отдельных точек твердого тела в Ц-системе оказывается сложной, за исключением немногих частных случаев. Мы не будем рассматривать эту задачу в общем виде и ограничимся в дальнейшем только отдельными частными случаями.

Но прежде приведем некоторые соображения, прямо выте­кающие из вида самих уравнений (1.9.1). Если мы будем переносить силы вдоль направления их действия, то ясно, что не изменяется ни их результирующая , ни их суммарный момент. При этом уравнения (1.9.1) тоже не изменятся, а следовате­льно, не изменится и движение твердого тела. Поэтому точки приложения внешних сил можно переносить вдоль направления действия сил — прием, которым постоянно пользуются.