Механической энергии.

Консервативные силы. Потенциальная энергия.

Если в каждой точке пространства на помещенную туда частицу действует сила, то частица находится в поле сил. Так, например, частица может находиться в поле сил тяжести, в поле упругих сил, в поле сил сопротивления (в потоке жидкости, газа) и т. д.

Поле, остающееся постоянным во времени, называют стационарным. Стационарное поле в одной системе отсчета может оказаться нестационарным в другой системе отсчета. В стационарном силовом поле сила, действующая на частицу, зависит только от ее положения.

Работа, которую совершают силы поля при перемещении частицы из точки 1 в точку 2, зависит, вообще говоря, от пути между этими точками. Вместе с тем имеются стационарные си­ловые поля, в которых работа, совершаемая над частицей силами поля, не зависит от пути между точками 1 и 2. Примеры таких сил были рассмотрены в предыдущей лекции. Силы, обладающие таким свойством, называют консервативными, а поле таких сил - потенциальным

Это свойство консервативных сил можно сформулировать и иначе: силы поля являются консервативными, если в стационарном случае их работа на любом замкнутом пути равна нулю.

Все силы, не являющиеся консервативными, называют неконсервативными. К числу неконсервативных сил относятся, например, силы трения и сопротивления – диссипативные силы. Работа этих сил зависит, вообще говоря, от пути между начальным и конечным по­ложениями частицы (и не равна нулю на любом замкнутом пути).

То обстоятельство, что работа консервативных сил в случае стационарного поля зависит только от начального и конечного положений частицы, дает возможность ввести чрезвычайно важное понятие потенциальной энергии.

Для всех рассмотренных в предыдущей лекции сил работа определялась через убыль потенциальной энергии, т. е. разность значений потенциальной энергии части­цы в начальной и конечной точках пути. Выражения (1.6.12), (1.6.13), (1.6.14) определяют потенциальную энергию соответственно в поле сил тяжести, упругости, гравитации.

Таким образом, работа сил потенциального поля на пути 1 — 2 равна убы­ли потенциальной энергии частицы в данном поле.

Очевидно, частице, находящейся в точке О поля, всегда можно приписать любое наперед выбранное значение потенциальной энергии. Это соответствует тому обстоятельству, что ра­бота сил поля определяет лишь разность потенциальных энергий в двух точках, но не их абсолютное значение. Однако как только фиксирована потенциальная энергия в какой-либо точке, значения ее во всех остальных точках поля определяются однозначно. Поэтому константу, входящую в формулу потенциальной энергии выбирают в зависимости от условий задачи. Так , для энергии гравитационной силы обычно полагают, что она равна нулю при бесконечном удалении тел, откуда следует, что 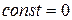; для силы упругости – энергия равна нулю при отсутствии деформации, откуда также 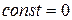; для силы тяжести в каждой задаче произвольно выбирают нулевой уровень энергии и тогда z - вертикальная координата, отсчитываемая от выбранного нуля. В последнем случае, если рассматривается протяженное тело, то z это координата его центра тяжести.

Отметим, однако, что тот факт, что потенциальная энергия U — функция, которая определяется с точностью до прибавления некоторой произвольной постоянной несущественнен, так как в формулы входит только разность значений U в двух положениях частицы. Поэтому произвольная постоянная, одинаковая для всех точек поля, выпадает.

И еще одно важное обстоятельство. Потенциальную энергию следует относить не к частице, а к системе взаимодействующих между собой частицы и тел, вызывающих силовое поле. При данном характере взаимодействия потенциальная энергия взаимодействия частицы с данными телами зависит только от положения частицы относительно этих тел.