Плоское движение твердого тела
При плоском движении центр масс C твердого тела движется в определенной плоскости, неподвижной в данной системе отсчета, а вектор его угловой скорости w все время остается перпендикулярным этой плоскости. Последнее означает, что в Ц-системе твердое тело совершает чисто вращательное движение вокруг неподвижной в этой системе оси, проходящей через центр масс тела. Вращательное же движение твердого тела определяется уравнением (1.9.7), которое, как было отмечено, справедливо в любой системе отсчета.
Таким образом, мы имеем следующие два уравнения, описывающие плоское движение твердого тела:
; 
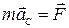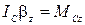(1.9.12)
где m — масса тела,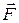 
— результирующая всех внешних сил, 
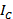и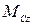 
— момент инерции и суммарный момент всех внешних сил — оба относительно оси, проходящей через центр масс тела.
Интегрируя уравнения (1.9.13) с учетом начальных условий, можно найти зависимости rC(t) и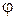 
(t), определяющие положение твердого тела в любой момент t.
При решении задачи о движении несвободного твердого тела необходимо использовать еще одно, дополнительное, условие, определяющее ограничения движения имеющимися связями. Оно дает кинематическую связь между линейным и угловым ускорениями.
Дата добавления: 2015-08-08; просмотров: 720;