Кинетическая энергия системы частиц.

Приращение кинетической энергии каждой частицы равно работе всех сил, действующих на частицу: ΔK_i = A_i. Поэтому работу A, которую совершают все силы, дей­ствующие на все частицы системы, при изменении ее состоя­ния, можно записать так: 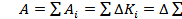К , или

(1.6.9)

где K — суммарная кинетическая энергия системы.

Итак, приращение кинетической энергии системы равно ра­боте, которую совершают все силы, действующие на все час­тицы системы:

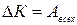(1.6.10)

Заметим, что кинетическая энергия системы — величина ад­дитивная: она равна сумме кинетических энергий отдельных частей системы независимо от того, взаимодействуют они меж­ду собой или нет.

Уравнение (1.6.10) справедливо как в инерциальных, так и в неинерциальных системах отсчета. Следует только помнить, что в неинерциальных системах отсчета кроме работ сил взаи­модействия необходимо учитывать и работу сил инерции.

Теперь установим связь между кинетическими энергиями системы частиц в разных системах отсчета. Пусть в неподвижной системе отсчета кинетическая энергия инте­ресующей нас системы частиц равна К. Скорость i-ой частицы в этой системе можно представить как, 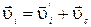, где 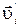— скорость этой ча­стицы в движущейся системе отсчета, a 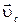—скорость движущейся системы относительно неподвижной системы отсчета. Тогда кинетическая энергия системы

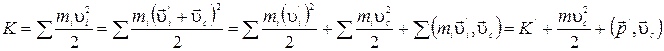где 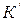- энергия в движущейся системе, т – масса всей системы частиц, 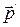- ее импульс в движущейся системе отсчета.

Если движущаяся система отсчета связана с центром масс (Ц-система), то центр масс покоится, а значит последнее слагаемое равно нулю и предыдущее выражение примет вид

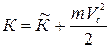, (1.6.11)

где 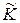— суммарная кинетическая энергия частиц в Ц-системе, называемая собственной кинетической энергией системы частиц

Таким образом, кинетическая энергия системы частиц складывается из собственной кинетической энергии и кинетической энергии, связанной с движением систе­мы частиц как целого. Это важный вывод, и он неоднократно будет использоваться в дальнейшем (в частности, при изучении динамики твердого тела).

Из формулы (1.6.11) следует, что кинетическая энергия сис­темы, частиц минимальна в Ц-системе. В этом еще одна осо­бенность Ц-системы.

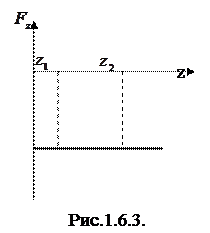Работа консервативных сил.

Воспользовавшись формулой (1.6.2) и

графическим способом определения работы,

рассчитаем работу некоторых сил.

1.Работа, совершаемая силой тяжести

Сила тяжести 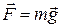направлена

вертикально вниз. Выберем ось z ,

направленную вертикально вверх и

спроецируем на нее силу .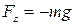

Построим график

зависимости 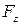от z (рис.1.6.3). Работа силы тяжести

при перемещении частицы из точки с координатой 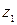в точку с координатой 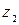равна площади прямоугольника

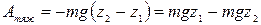
Как видно из полученного выражения работа силы тяжести равна изменению некоторой величины, не зависящей от траектории частицы и определенной с точностью до произвольной постоянной

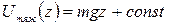. (1.6.12)

2.Работа силы упругости.

Проекция силы упругости на ось х, указывающую направление деформации,

,

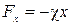где х – величина деформации, отсчитываемая

от недеформированного состояния.

График этой функции от величины

деформации х приведен на рис.1.6.4.

Тогда работа силы упругости при

изменении деформации от 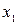до

определится площадью трапеции

.

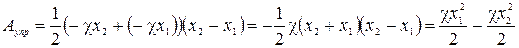Таким образом, и для силы упругости работу можно представить как изменение некоторой величины, зависящей от начального и конечного состояния

. (1.6.13)

3.Работа гравитационной силы.

Без вывода приведем работу еще одной силы, которая подчиняется тем же закономерностям. Это обобщение силы тяжести - гравитационная сила

,

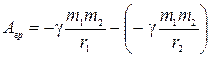где 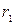и 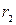- начальное и конечное расстояние между частицами. То есть, и в этом случае работу можно представить через изменение функции

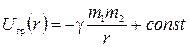. (1.6.14)