Где — скорость Ц-системы относительно K-системы. Поэто­му

. (1.5.16)

Первая сумма в правой части этого равенства есть собственный момент импульса . Вторую сумму представим в соответствии с формулой (1.4.5) как или , где m — масса всей системы, — радиус-вектор ее центра масс в K-системе, — суммарный импульс системы частиц. В результате

, (1.5.17)

Т. е. момент импульса системы частиц складывается из ее собственного момента импульса и момента, обусловленного движением системы частиц как целого.

Возьмем, например, однородный шар, скатывающийся по наклонной плоскости. Его момент импульса относительно некоторой точки этой плоскости складывается из момента импуль­са, связанного с движением центра масс шара, и собственного момента импульса, обусловленного вращением шара вокруг собственной оси.

Из формулы (1.5.17), в частности, следует, что если центр масс системы покоится (импульс системы равен нулю), то ее момент импульса — это собственный момент импульса. С этим случаем мы уже знакомы. В другом крайнем случае, когда 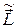= 0, момент импульса системы относительно некоторой точки определяется только моментом, связанным с движением системы как целого, т. е. вторым слагаемым (1.5.17). Так, например, ведет себя момент импульса любого твердого тела, совершающего поступательное движение.