Связь между потенциалом и напряженностью электростатического поля. Эквипотенциальные поверхности.

Как ранее показано, работа сил электростатического поля при перемещении за­ряда q₀ может быть записана с одной стороны, как 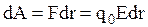, с другой же - как убыль потенциальной энергии, т.е. 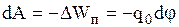. Здесь dr - есть проекция элементарного перемещения dl заряда на направление силовой линии 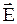, - есть малая разность потенциалов двух близко расположенных точек поля. Приравняем правые части равенств и сократим на q₀ . Получаем соотношения

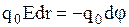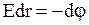, . Отсюда .

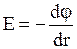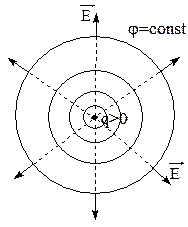Рис.1.13. Эквипотенциа­льные поверхности (сплошные) и силовые линии (пунктирные) поля точечного поло­жительного заряда.

Последнее соотношение представляет связь ос­новных характеристик электро­статического поля Е и j. Здесь 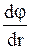- быстрота изменения потенциала в направле­нии силовой линии. Знак ми­нус указывает на то, что вектор 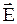направлен в сторону убывания потенциала. Поскольку 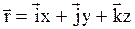, можно записать проекции вектора 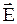на координатные оси: 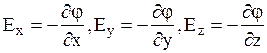. Отсюда следует, что 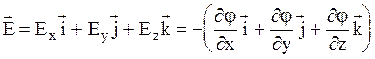. Выраже­ние, стоящее в скобках, называется градиентом скаляра j и обозначается как gradj.

Напряженность электростатического поля равна гра­диенту потенциала, взя­тому с обратным знаком .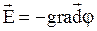

.

Для графического изображения распределения потенциала электростатичес­кого поля пользуются эквипотенциальными поверхностями - поверхностями, потен­циал всех точек которых одинаков. Потенциал поля одиночного точечного заряда . Эквипотенциальные поверх­нос­ти в данном случае есть концентрические сферы с центром в точке расположе­ния за­ряда q (рис.1.13). Эквипотенциальных поверхностей можно провести бесконеч­ное множество, однако принято чертить их с густотой, пропорциональной величине Е.