Применение теоремы Гаусса для расчета напряженности электростатического поля.

1. Поле равномерно заряженной бесконечной плоскости с поверхностной плотностью зарядов +s.

Пусть поверхностная плотность зарядов или заряд, приходящийся на единицу поверхности 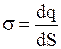. Силовые линии поля перпендикулярны этой плоскости и направлены от нее в обе стороны (рис.1.10).

Построим замкнутую цилиндрическую поверхность с основаниями dS, парал­лельными заряженной поверхности и образующей, параллельной вектору 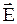. Сле­дуя последнему условию, поток напряженности Ф_Е через боковую поверхность ци­линдра равен нулю. Поэтому полный поток через цилиндрическую поверхность ра­вен сумме потоков сквозь его основания. Так как вектор 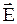перпендикулярен осно­ваниям, Е_n=Е и суммарный поток Ф_Е можно записать Ф_Е=2ЕdS.

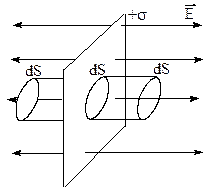Рис.1.10. Определение на­пряженности поля беско­нечной заряженной плос­кости.

Согласно теореме Гаусса 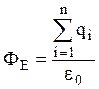, где 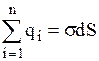- заряд, охватываемый цилиндрической по­верхностью. Таким образом

, .

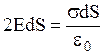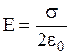Если плоскость помещена в среду с относительной ди­электрической проницаемостью e, то напряженность электростатического поля, соз­даваемая плоскостью, равна .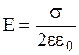

Из формулы следует, что Е не зависит от расстояния между плоскостью и точкой на­блюдения, т.е. поле равномерно заряженной бесконечной плоскости однородно.

1. Поле двух бесконечных разноименно заряженных плоскостей.

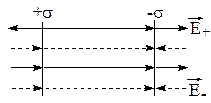Рис.1.11. Определение на­пряженности поля двух параллельных разноимен­но заряженных плоско­стей.

На рис.1.11 перпендикулярно чертежу располо­же­ны две такие плоскости с поверхностными плотно­стями за­рядов +s и -s. Силовые линии плоскостей перпенди­ку­лярны им и параллельны между собой. Силовые ли­нии выходят из плоскости +s и входят в плоскость ‑s. На ри­сунке сплошными стрелками изо­бражено поле плоскости +s и пунктирными - поле плоскости -s.

Напряженности полей обеих плоскостей равны по абсолютной величине 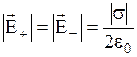. Однако, справа и слева от плоскостей напряженности 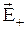и направлены проти­во­положно, поэтому суммарная Е=0 и поле отсутствует. В области между плоскос­тями 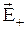и направлены одинаково, поэтому .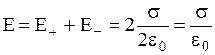

1.10. Работа сил электростатического поля при перемещении заряда.

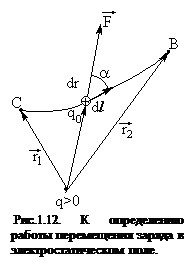
При перемещении заряда в электростатическом поле, действующие на заряд кулоновские силы, совершают работу. Пусть заряд q₀>0 перемещается в поле заряда q>0 из точки С в точку В вдоль произвольной траектории (рис.1.12). На q₀ действует кулоновская сила

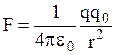. При элементарном перемещении заряда dl, эта сила совер­шает работу dA

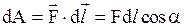, где a - угол между векторам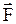и и 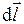. Величина dlcosa=dr является про­екцией вектора 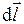на направление силы 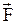. Таким образом, dA=Fdr, 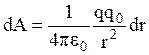. Полная работа по перемещению заряда из точки С в В определяется интегра­лом 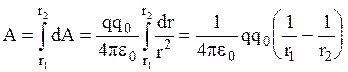, где r₁ и r₂ - расстояния заряда q до точек С и В. Из полученной формулы следует, что работа, совершаемая при перемещении электрического заряда q₀ в поле точеч­ного заряда q, не зависит от формы траектории перемещения, а зависит только от начальной и конечной точки перемещения.

В разделе динамики показано, что поле, удовлетворяющее этому условию, яв­ляется потенциальным. Следовательно, электростатическое поле точечного заряда - потенциальное, а действующие в нем силы - консервативные.

Если заряды q и q₀ одного знака, то работа сил отталкивания будет положи­тельной при их удалении и отрицательной при их сближении (в последнем случае ра­боту совершают внешние силы). Если заряды q и q₀ разноименные, то работа сил притяжения будет положительной при их сближении и отрицательной при удалении друг от друга (последнем случае работу также совершают внешние силы).

Пусть электростатическое поле, в котором перемещается заряд q₀, создано сис­темой зарядов q₁, q₂,...,q_n. Следовательно, на q₀ действуют независимые силы 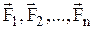, равнодействующая которых равна их векторной сумме. Работа А рав­но­действующей силы равна алгебраической сумме работ составляющих сил, 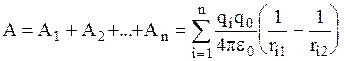, где r_i1 и r_i2 - начальное и конечное расстояния между зарядами q_i и q₀ .