ЛИНЕЙНЫЕ ПРОСТРАНСТВА
Введем математические объекты: S - множество векторов: х,y,z....; К - множество скаляров:l, m, e ..;
Линейное пространство S над полем К определяется как система:
Р = (S, К;j, h),
где j: S ´ S ® S- внутренний закон композиции (аддитивный), S образует абелеву группу, т.е. коммутативную, ассоциативную, с нейтральным (нулевым) и обратным (-х) элементами;
h: K ´ S ® S - внешний закон композиции со свойствами:
а) дистрибутивности относительно внутреннего закона сложения векторов: l(х + у) = lx + ly ;
б) дистрибутивности относительно аддитивного закона поля К (сложения скаляров): (l + m)x = lx + mх,
в) ассоциативности относительно мультипликативного закона поля К: (lm)x = (lx)m;
г) наличие нейтрального элемента (e) относительно умножения в поле К: ex = x.
Линейные пространства S над полем К могут быть действительными или комплексными, если К соответственно поле действительных или комплексных чисел.
Примеры
1. 3-мерные векторы х(х1;х2;х3) образуют действительное линейное пространство j: х + у = z; h:lx.
2. Если S = К, то любое поле К можно рассматривать как векторное пространство над самим собой: j: (+); h:(*).
3. S = {а, b, c}; j: S ´ S ® S; j º (+).
| j | a | b | c |
| a | b | c | a |
| b | c | a | b |
| c | a | b | c |
Здесь С - нейтральный элемент. Структура типа "абелева группа".
Постройте граф отношения для заданного j.
4. S = {а, b, с), К = {1, 2, 3} - имеем поле вычетов по модулю 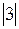 .
.
Поле вычетов можно задать в виде таблиц отношений:
| * | a | b | c | (+) | (*) | ||||||
| c | c | c | |||||||||
| a | b | c | |||||||||
| b | a | c | |||||||||
| K ´ S ® S |  K ´ K ® K K ´ K ® K
|
Дата добавления: 2015-07-30; просмотров: 734;
