ПРОСТРАНСТВА И ПРОСТРАНСТВЕННО -ПОДОБНЫЕ ОТНОШЕНИЯ
Основные системные свойства пространства:
1) структурность, т.е. единство прерывности и непрерывности;
2) протяженность;
3) неразрывность от движения;
4) неотделимость от материи и времени;
5) количественная и качественная бесконечность.
Пространство "П" определяется как система в виде математической структуры:
-постулируются свойства пространства;
-определяются элементы пространства на теоретико-множественном уровне;
-вводится система отношений: Р º П = (М,R1,R2;...) Û (А;R),
где П или Р - знак пространства;
М - множество элементов пространства;
R = {Ri} - множество отношений между элементами.
Примеры математических пространств: евклидово, параметрическое, векторное (гильбертово).
Гильбертово пространство обобщает свойства евклидова пространства на бесконечно - мерный случай.
Пример 1. Евклидово пространство
М = {(х;у;z)}; 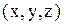 - координаты точки (объекта),
- координаты точки (объекта),
R1 = 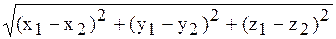 - расстояние между объектами.
- расстояние между объектами.
Пример 2. Векторное пространство
M = { 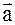 };
}; 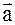 Î N3 = N*N*N;
Î N3 = N*N*N; 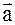 = (х,у,z);
= (х,у,z);
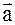 - вектор из точки (0,0,0) в точку (х,у,z);
- вектор из точки (0,0,0) в точку (х,у,z);
R1 = 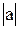 =
= 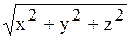 - длина вектора;
- длина вектора;
R2 = 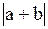 =
= 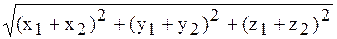 - длина суммарного вектора;
- длина суммарного вектора;
R3 = 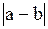 =
= 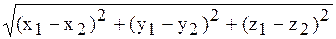 - длина вектора разности 2-х векторов;
- длина вектора разности 2-х векторов;
R4 = ab = 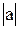
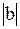 cos(a,b) =х1х2 + у1у2 + z1z2 - векторное произведение;
cos(a,b) =х1х2 + у1у2 + z1z2 - векторное произведение;
R5 Û cos(a,b) = 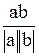 =
= 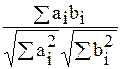 ;
;
R6 Û {орты} = {i = (1,0,0);j = (0,1,0);k = (0,0,1)};
R7 Û а = (х,у,z) = xi + уj + zk.
П = ({х,у,z}; R1; R2; R3; ... ; R7; ...).
Отметим примеры специальных типов пространств: функциональные пространства и пространства нечисловой природы. Например, трехцветное векторное пространство, применяемое в цветном телевидении, многоцветные психологические тесты (тест Люшера), пространство переменных состояний, пространство толерантности…
3.1.1. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
(ГИЛЬБЕРТОВО ПРОСТРАНСТВО)
Для метрического пространства вводятся свойства метрики в виде системы аксиом (b) :
1. b(x,у) ³ 0; b(x,x) = b(y,у) = 0.
2. b(x,у) = b(y,x) - симметричность.
3. b(x,у) £ b(y,x) + b(y,z) - свойство треугольника.
П = (М; b); х,у Î М, b Î R.
Частные случаи отношений для метрических пространств:
b1(x,у) = 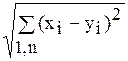 - расстояние в n-мерном пространстве.
- расстояние в n-мерном пространстве.
b2(x,у) = 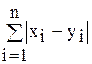 - расстояние по сумме разностей координат.
- расстояние по сумме разностей координат.
b3 = mах 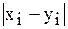 - максимальное расстояние между границами пространства, используется для перехода к нормированным метрическим пространствам .
- максимальное расстояние между границами пространства, используется для перехода к нормированным метрическим пространствам .
Дата добавления: 2015-07-30; просмотров: 900;
