СИСТЕМНАЯ ПАРАДИГМА
По определению общая теория систем (ОТC) - наука об универсальных законах и принципах, распространяющихся одновременно на биологические, физические, социальные и др. явления.
До 1960 г. выделялись три ведущие школы в ОТС. Первая связана с именем Людвига фон Берталанфи и его последователей (1930 г.). В этой школе ОТС рассматривается как некоторая философия науки, изучающая функциональные междисциплинарные знания. Общая теория систем в начале противопоставлялась классической математике: ”создание математической общей теории систем противоречит, по мысли авторов, основным понятиям общей теории систем”. Развитие дискретной математики снимает это противоречие.
Вторая школа связана с именем Норберта Винера (1948 г.) и его последователей, разработавших кибернетический подход в системных исследованиях на основе понятия управления. Изучение процессов управления имеет междисциплинарный характер. Это основа для информационных управляющих систем и первый реальный пример междисциплинарных исследований в области управления.
Третья школа связана с понятием “сложной системы”. Представители этого направления: Герберт Саймон, Вл. Ив. Вернадский. Сложные системы: социальные, политические, экономические, искусственные и естественные. Идеи оптимизации здесь неприменимы из-за сложности и противоречивости протекающих процессов. В лучшем случае можно выделить типичные ситуации.
Дальнейшее развитие науки и вычислительной техники определило ход развития ряда направлений в теории систем, такие как:
· абстрактная теория систем (Месарович, Такахара) [29];
· информационные системы (К.Эшби) [9];
· динамические системы (Калман, Арбиб) [26];
· системология (Клир) [1].
В системологии Дж. Клира выделяются три периода в истории науки о системах и вводится понятие о втором измерении в науке, т.е. двумерности научных знаний. Рассмотрим эти периоды.
Первый период. Донаучный (до 16 в.), допарадигмальный. Его характерные черты: в основе исследований лежит метод проб и ошибок, здравый смысл, случайный поиск и эвристический подход, ремесленничество в лучшем смысле этого слова, сила традиций, дедуктивность рассуждений.
Второй период. Одномерная наука (начало 17 и середина 20 веков.). Развитие эмпирических знаний и научных дисциплин, таких, как физика, химия, математика, механика; опора на эксперимент; "живой опыт" - мера познания. Идет накопление знаний и данных по отдельным наукам.
Третий период -современный. Двухмерность в науке. Дополнительно к опыту, эксперименту появляется второе измерение - интегрирование и абстрагирование знаний о системах различной природы. Системная парадигма знаний становится определяющей.
Двухмерность проявляется в изучении отношений самого общего вида, пространственно-подобных отношений, толерантности и эквивалентности, управляемости, сложности, инвариантности, вычислимости, формализуемости...
Двухмерность возникла в ходе развития одномерных знаний. Например, в физике можно выделить следующие этапы:
· организованная простота (механика);
· беспорядочная сложность (статистическая физика);
· организованная сложность (система знаний).
Итак, одномерность - это преобладание эмпирического подхода (физика, химия, биология...); двухмерность - это преобладание рационального подхода (исследование операций, кибернетика, системотехника, системология). Двухмерность, как методология изучения, проникает в современные подходы к освоению одномерных научных дисциплин.
Теория систем является частью теории познания, основой эпистемологической ее ветви.
ОТС зародилась в 1930-х годах; в 1950-х годах сформировалась в научное направление ( в широком смысле слова).
Формализованный аппарат разрабатывался с 1948 г. для задач управления. В 70-х годах предложена абстрактная теория систем на основе алгебраизации математического аппарата описания общей теории систем.
До 1954 г. (период осмысления) был похож на "заговор молчания" в ученом мире.
В 1954 г. создано "общество исследователей в области общей теории систем" . Организаторы : Л. Берталанфи, Р. Жерар, А. Раппопорт, К. Боулдинг.
В 1968 г. составляющими ОТС по Берталанфи были следующие научные дисциплины:
1. Теоретические (множества, графы, сети, автоматы).
2. Специальные (теории: массового обслуживания, информации, игр, статистических решений, распознавания и классификации).
3. Прикладные (кибернетика, вычислительная техника, системотехника, исследование операций, социальная психология, лингвистика, метасистемы, системы знаний).
В 1996 году подобная классификация не может быть парадигмой ОТС. Многие дисциплины за это время превратились в самостоятельные научные направления, например, вычислительная техника, лингвистика. Ряд специальных дисциплин сформировал прикладное направление в науке, получившее название "Исследование операций и системный анализ". В настоящее время и математика ориентирована на дискретные методы и машинные средства обработки информации.
С другой стороны, системный подход конкретизировал круг задач для теории систем, как методологической составляющей общей теории систем.
Аналогами понятия "теория систем" выступают "эпистемология", "теория познания" со смысловым оттенком познавания, т.е. системология организации познавательного процесса.
Для специальностей 220200 теория систем связана с процессом формирования систем представления и обработки информации, с инженерией знаний.
Задачи и упражнения
1. В приложении П.1 приведено описание объекта физической природы типа "Прессдуктор". Имя объекта и форма была предложена шведской фирмой АSЕА. Объект является простым и надежным чувствительным элементом преобразователей силы (F) и давления (Р) в электрический сигнал. Процесс преобразования силового параметра имеет сложный характер электромагнитомеханического взаимодействия трех видов полей: электрического, магнитного и механического.
Ознакомьтесь с данным описанием объекта. На основе
рис. П. 1.2 и П. 1.3; проведите системный анализ объекта.
Вопросы к системному анализу.
1.1. Представьте объект в виде кибернетической системы.
1.2. Определите классы допустимых входных воздействий.
1.3. Сформулируйте цели и задачи исследований (экспериментов).
1.4. Перечислите ПОЗ, связанные с системным анализом объекта.
1.5. Определите предметные области деятельности, связанные с системным анализом объекта.
1.6. Определите возможные каналы наблюдений и воздействий на объект.
1.7. Какие свойства характеризуют объект, как направленную динамическую систему?
1.8. Опишите понятие “идеальный случай” для состояния F(t)=0.
1.9. Являются ли номера отверстий базой для идентификации при описании объекта?
1.10. Определите понятия, введенные для неинтерпретированной общей системы, для рассмотрения объекта наблюдений. При необходимости примените операции конкретизации и абстрагирования.
1.11. Как метаоперации и операции абстрагирования отражаются при описании схемы объекта в случае гармонического воздействия?
2. В приложении П.2 приведено описание объекта, связанного с процессом обучения студентов в ВУЗe. Рассматривается часть традиционной системы типового учебного процесса: лекции, практические занятия, лабораторные работы, зачеты и экзамены. ВУЗ является объектом социальной природы, характер процессов в котором в лучшем случае можно свести к описанию вероятностными системами и моделями.
По аналогии с упр.1 примените системный подход для приведенного объекта наблюдений (см. П.2). Конкретизируйте вопросы к системному анализу объекта.
3. Определите толковый словарь исходных понятий теории систем по первоисточникам для следующих понятий: системный подход, системный анализ, объект, субъект, система, задача, теория, системный анализ, модель. Систему использованных первоисточников выделите из списка литературы, прилагаемого к пособию.
3.1. Рассмотрите эти понятия .как лингвистические объекты наблюдений с позиции системного подхода.
3.2. Выделите определяющие свойства объектов наблюдений, позволяющие объединять их в общем понятии "теория систем".
4. Для исходного понятия, например: "систем общая теория", постройте семантическую сеть, иллюстрирующую систему ссылочных отношений с другими понятиями. Для этого выделите первоисточник с указанной статьей в энциклопедии кибернетики [3].
5. В приложении П.3 приведены высказывания на формализованном языке в виде систем уравнений. Определите данные высказывания как отдельные системы и как их комплексы. Выделите элементы, отношения, параметры, переменные. Какими типами рациональных систем являются данные предложения? Какими средствами дискретной математики можно проиллюстрировать структурность приведенной системы высказываний?
ГЛАВА 2. ОТОЖДЕСТВЛЕНИЕ ОБЪЕКТА
НАБЛЮДЕНИЙ С СИСТЕМОЙ
Идентификация объекта связана с абстракцией отождествления. Идентификация - это "установление соответствия распознаваемого объекта своему образу (знаку)" [32].
Имя предмета, множество описаний его свойств и отношений, выделение существенных признаков для определения классов понятий и отношений являются средствами "групповой идентификации" объекта наблюдений в среде и между объектами, т.е. являются средствами базирования в смысле {(Вj;bj)}.
Для идентификации и группового базирования применяются рациональные системы описаний на уровнях У1;У2;У3;У4.
Французское слово "база" и греческое "базис" означают основу чего-либо, основание, фундамент, в данном случае основа для идентификации объекта наблюдения среди множества других.
От базы, как от основания, можно строить систему описаний и моделей объекта наблюдений.
В качестве базиса (базы) используются три понятия:
· групповое описание, идентифицирующие объект наблюдений, как предмет, вещь, событие, мероприятие, исследуемую операцию (Г; G);
· пространственное описание объекта в среде по отношению к другим объектам и процессам, (П или Р);
· временное или время-подобное описание поведения объекта в пространстве наблюдений, в пространстве состояний и переходов (В; Т).
Рассмотрим уровни описания объекта для его группового базирования, т.е. отождествления объекта, как части мира, выделенной субъектом для наблюдений.
2.1. СИСТЕМА НА ЗНАКОВО-ЛИНГВИСТИЧЕСКОМ УРОВНЕ - У1
На лингвистическом уровне имена предметов называют термами.
Отношения между термами описываются с помощью функторов.
Итак, множество понятий, связанных с объектом наблюдений, разбиваются на два типа подмножеств: на термы и функторы.
Знания субъекта об объекте наблюдений формируются в виде множества правильных высказываний. Сами термы и функторы также определяются как правильные высказывания.
Под правильным высказыванием понимается утвердительная форма предложения, истинность или ложность которого определена субъектом логически или операционно (по каналу наблюдений или каналу абстрагирования).
При описании объекта на уровне У1 некоторые термы могут варьироваться субъектом, т.е. определяются как константы, задаваемые субъектом в процессе конкретизации наблюдений. Подобные термы в общем случае называются конституэнтами.
В качестве конституэнт выступают, в частности, физические константы, коэффициенты уравнений, параметры среды наблюдений и т.п.
Из термов, конституэнт и функторов строят предложения (высказывания), которые могут быть истинными при определенных значениях конституэнт.
В общем случае множество высказываний образует систему правильных высказываний (П), часть из которых истинная (Т).
Если конституэнты в Т-высказываниях являются формально определяемыми величинами, то множество правильных высказываний Т на множестве П образует теорию.
На лингвистическом уровне (по Месаровичу) система (å1) определяется как множество правильных высказываний, построенных из термов и функторов: [29]
S Û å1=(A;R)=({термы, конституэнты};{функторы}).
Задачи и упражнения
1. Для работ, проводимых в огороде в мае месяце для картофеля, в таблице Жукова находим следующую систему высказываний.
"В мае продолжают проращивать до посадки поздний картофель. С 1 по 5 мая сажают рассаду раннего картофеля под пленку (на случай заморозков). При температуре почвы +(8-10 С°) сажают клубни по схеме 60´ЗО´6 см; при посадке опыляют золой. 15-25 мая сажают поздние сорта. При росте кустиков в 20 см окучивают, предварительно удобряя и увлажняя почву".
а. Является ли данное множество высказываний правильным в общем случае и по Месаровичу?
б. Выделите термы, конституэнты и функторы. Определите арность отношений, описываемых функторами.
в. Выделите признаки (свойства), как унарные отношения, определяемые прилагательными.
г. Конкретизируйте понятия: объект, субъект, система объекта на данном примере.
2. Базовыми понятиями теории систем являются: объект, субъект, системный подход, система, задача субъекта, модель, системный анализ.
…. Известны определения данных понятий по первоисточникам.
а. Исследуйте по первоисточникам одно из этих понятий как систему, описываемую с помощью термов и функторов: учтите, что термами и функторами при описании каждого понятия выступают другие понятия.
б. Определите множество истинных высказываний для указанной совокупности понятий, которое можно принять в качестве основы теории систем (на лингвистическом уровне).
в. Предложите описание отношений понятий в данной теории в виде графа: Г(Х;У), где X - вершина графа (понятия); У - ребра графа (отношения между понятиями), петли - унарные свойства понятий.
3. Определите отличительные признаки понятий: теория, интуитивная теория, аксиоматическая теория, дополнив систему правильных высказываний о формальных теориях и математических структурах [65].
4. Теория матричных игр строится на таких понятиях как конфликтная ситуация, игроки, стратегия, пространство стратегий, ход, выбор, исход, выигрыши, потери, партия игры, функция потерь, правила игры [20; 24].
Постройте систему для описания матричных игр на лингвистическом уровне, т.е. как множество правильных высказываний, используя первоисточники, например [20].
5. Имитационное моделирование трехканальной системы массового обслуживания в учебном пособии [21] рассмотрено на конкретной системе типа G/G/3/3.
Составьте описание этой конкретной системы на лингвистическом уровне в виде исходного множества правильных высказываний, определяющих поведение объекта в среде наблюдений.
2.2. ТЕОРЕТИКО-МНОЖЕСТВЕННЫЙ УРОВЕНЬ
ОПИСАНИЯ СИСТЕМЫ - У2
Система как множество правильных высказываний X может быть представлена в виде разбиения исходных множеств на подмножества:
X = 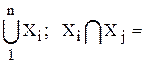 Æ ;
Æ ;
Каждое подмножество Xi также представляет собой систему элементов хi Î Хi со своими свойствами и отношениями.
Из множества систем можно сформировать в общем случае систему Хs, как собственное подмножество указанных множеств:
Ms Í M=Х1 ´ X2 ´ …Хn={(X)}, (2.1)
где Х = (х1, х2, ... хn);
X - кортеж, вектор, последовательность (в зависимости от свойств объекта).
Объект X может быть точкой в n-мерном пространстве (математический объект) или описанием конкретного объекта по множеству признаков (быть базой для идентификации объекта).
Итак, система на уровне абстрагирования У2 представляет собой собственное подмножество (МS) множества М, определенного на прямом произведении множеств Х1; Х2; …Хn. При этом решается задача распознавания и классификации термов на уровне множеств. Функторы определяются в отношениях на множествах. Вводится соответствующая система обозначений множеств и их элементов.
Задачи и упражнения
1. Определите на примере таблицы Жукова (см. упр. п.2.1) базовые множества вида Х1 ´ Х2 и возможные подмножества Хs Ì X1 ´ Х2. В чем проявляется сходство описаний таблицы Жукова и индикатора символов с числом ячеек m ´ n?.
2. Известно определение множества по Н. Бурбаки: "Множество образуется из элементов, обладающих некоторыми свойствами и находящимися в некоторых отношениях между собой или с элементами других множеств".
Пусть объект представляет собой индикатор для визуализации множества символов размера 7 ´ 5. Подобные индикаторы применяются в различных реальных устройствах. Множество элементов индикатора равно 35 и упорядочено в пространстве 5 ´ 7, как показано на рисунке.
Х2
| X1 | ||||||
|
 |

а. Опишите работу одного из этих устройств в виде системы правильных высказываний.
б. Определите свойства элементов для выделенных на индикаторе трех множеств Х1 = {1; …7}; Х2 = {1;...5}; Х3={1;...35}.
в. Приведите содержательное описание систем типа
МS Í Х1 ´ X2 ´ …Хn, в которых используется индикатор символов.
г. Понятие "множество" (по Бурбаки) является системой. Проиллюстрируйте это с помощью понятия "граф". Для этого термы определите как вершины графа, а функторы - как петли, ребра или дуги графа.
3. Дано Х = Х1 ´ X2 ´ …Хn = {(х1;х2;...хn)},
определите значение понятий:
ПрiX; ПрjХ; Прi,l,kХ , здесь Пр - проекция.
2.3. АБСТРАКТНО - АЛГЕБРАИЧЕСКИЙ УРОВЕНЬ
ОПИСАНИЯ - У3
Этот уровень абстрагирования - конкретизации связан с математическими объектами типа:
Г: М1 ´ М2 ´...Мn ® Мn+1; М Ì N,
где Г- обозначение математической структуры и алгебраической операции (в зависимости от смыслового оттенка утверждения);
{М}- базовые множества Г структуры (носители структуры);
{´; ®}- обозначение системы отношений, определенной на базовых множествах (произведение множеств и следование);
N - упорядоченное множество элементов, например, множество натуральных чисел, кортеж событий, алфавит символов ....
Конкретизируя систему свойств и отношений, например, в виде наборов постулатов (системы аксиом) получим, в частности, абстрактно-алгебраические структуры типов: группоида, полугруппы, группы, кольца, модуля, тела, поля, решетки ...., которые определяют целые классы формальных систем вида:
S = (M1; M2; ;p1;p2; ;a1; a2);
здесь:
S - алгебраическая система (математическая структура);
{М}- базовые множества определения системы;
{р}- отношения, определенные на элементах множества;
{a}- свойства, образующие систему аксиом К(a) или систему истинных утверждений (теорию в смысле лингвистического подхода).
Система отношений {р} может определяться на множествах: R1;R2;R3;...Rn типов отношений, где индекс обозначает "арность" или "местность" отношения:
R1 - множество унарных /одноместных отношений;
R2 - множество бинарных /двухместных отношений;
…
Rn - множество энарных /энместных отношений.
С помощью R1, в частности , описывается общее свойство элементов из данного множества-универсума по выделенному свойству.
Примерами бинарных отношений являются композиции, соответствия, отношения, отображения, в которых паре элементов ставится в соответствие третий элемент [2].
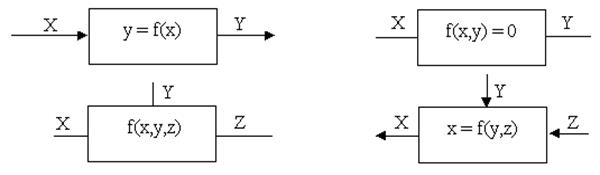
Функции (функционалы, операторы) являются классами объектов, определяемых на различных уровнях отношений:
У = f(x) или f(x,У) = 0 - двухместное отношение;
z = f(x,У) или f(x,У,z) = 0 - трехместное отношение;
q = f(x,У,z) или f(x,У,z,q) = 0 - четырехместное отношение.
Схема представления функции имеет вид направленной или ненаправленной кибернетической системы:
Итак, понятие системы на абстрактно-алгебраическом уровне конкретизируется с учетом уровней У1 и У2. На уровне У1 определяется теория, как множество правильных высказываний о свойствах объекта исследований {a}. На уровне У2 конкретизируется множество элементов и их отношений {М}. Множество подмножеств {М} выбирается в качестве базы. На уровне УЗ конкретизируется понятие алгебраической операции в виде системы отношений {р}.
Задачи и упражнения
1. Свойствами математических объектов, в частности, являются: рефлексивность (1), антирефлексивность (2), симметричность (3), антисимметричность (4), несимметричность (5),транзитивность (6) :
{р1;р2; ... р6} [2] .
Проиллюстрируйте указанные свойства в виде систем отношений на графах и на матрицах для множества из 4-х элементов {а,b,с,d}.
2. Известны системы отношений: эквивалентность (1), предпорядок (2), порядок нестрогий (3), строгий порядок (4), толерантность (5), доминирование (6).
а. Составьте таблицу свойств для этих отношений в виде алгебраической абстракции операций вида Х ´ Y ® А и Y ´ X ® В
при Х = У = {1,2,3,4,5,6}, если принять, что X - свойства, У - отношения, А = В = {0;1} в смысле "быть или не быть" свойству в данном отношении.
б. Сравните свойства таблиц А и В.
в. Определите модели систем, представляющие указанные отношения на графах и матрицах.
3. В понятиях групповых структур одинакового порядка изоморфизм определяется наличием двух свойств одновременно: инъекции и сюръекции. Говорят в этом случае о биективном (двойном) отображении.
Гомоморфизм имеет место при наблюдении одного из указанных свойств и разделяется на мономорфизм (при инъекции) или эпиморфизм (при сюръекции).
Определите изоморфизм понятий и схему соответствий для физических и математических систем, описываемых уравнениями:
L 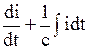 + Ri = V- электрическая система;
+ Ri = V- электрическая система;
ma + kv + ws = F - механическая система;
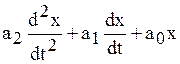 = f(x) - математическая система.
= f(x) - математическая система.
Определите понятие модели на основе свойства изоморфизма.
4. Для групповых операций мультипликативности и аддитивности на множестве {а,b,с} запишите алгебраические законы: сочетательный (ассоциативный), переместительный (коммутативный) и распределительный (дистрибутивный). Определите понятия нейтрального и обратного (противоположного) элементов.
5. Алгебраическая система задана таблицей: Х ´ У ® У1
Здесь Х = У = У1 = {0,1,2,...6}.
Мощность множеств равна:
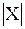 =
= 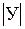 = 6
= 6
Таблицу можно рассматривать как одно из возможных высказываний. Какова мощность источника высказываний для системы аргументов X и У?
6. Определите классы отношений и их интерпретацию для системы знаков:
{=; º; ~; «;½½; ^; <; £; ³; >; Î; Í; È; Ç; ¤; Þ; Û} .
Дополните систему знаков известными Вам и выделите неизвестные.
7. Алгебраическая система типа Т: А ´ А ® А называется композицией объектов. Композиция может быть представлена таблицей или графом композиции, например:
| Т0 | a | b | c | 
|
| a | b | c | a | |
| b | c | c | b | |
| c | b | b | c |
Постройте граф композиции для следующего комплекса систем Т:
| Т1 | a | b | c | d | e | T2 | b | c | T3 | a | b | c |
| a | e | a | e | a | a | a | c | b | a | b | c | a |
| b | c | c | b | c | d | b | b | a | b | c | a | b |
| c | e | d | d | d | b | b | a | c | c | a | b | c |
| d | b | d | b | b | a | |||||||
| e | c | b | d | e | a |
К какому классу алгебраических систем относятся системы
Т1, Т2, Т3?
2.4. ЛОГИКО-МАТЕМАТИЧЕСКИЙ УРОВЕНЬ
ОПИСАНИЯ СИСТЕМ - У4
Логико-математическая интерпретация алгебраического уровня описания достигается путем идентификации значений истинности и ложности и их модальностей на отрезке [0,1], как универсуме.
Для положительной двухзначной логики без модальностей - это крайние точки отрезка: 0 - ложно, 1- истинно.
При этом значения аргументов и функции определяются на одном и том же множестве {0,1}.
|
| q1 | q2 | q3 | q4 | ||||
  0 0
| ||||||||
| x1 | x2 | q1 | q2 | … | q16 | |
| … | ||||||
Логическая операция в общем случае записывается, как частный случай алгебраической:
j: 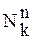 ® Nk; Nk = {0,1,2,3,…,k-1},
® Nk; Nk = {0,1,2,3,…,k-1},
где k - значность логики, определяется мощностью NK .
Для двузначной логики N2 = {0;1}, т.е. мощность множества  = 2, или из уравнения k-1=1, следовательно k=2.
= 2, или из уравнения k-1=1, следовательно k=2.
Логическая интерпретация определяет систему отношений элементов множества Nk к областям истинности и ложности. Кроме положительной, различают отрицательную и смешанные типы логик.
Если ввести десятичный эквивалент двоичных наборов и использовать его для упорядоченного описания номеров наборов аргументов и номеров функций, то алгебраической базой описания логического пространства являются алгебраические выражения вида:
j: 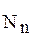 ® Nm,
® Nm,
где n - число аргументов;
Nn - число наборов аргументов;
Nm - число логических функций.
Для двухзначной логики имеем:
Nn Î {0,2,4,8, … q}; q = 2n; Nm = {0,2,4,8,16,32 ...,r}; r = 2q.
Для k - значной логики q = kn и r = kq.
Таким образом, формально между допустимыми множествами значений Nn и Nm для двухзначной логики имеется степенная зависимость вида
| n | ||||||
| Nn | ||||||
| Nm | ……. |
Для идентификации функций при n = 4 по десятичным номерам удобно использовать модель логического пространства в виде карты Карно:

| XY | |||||||||||||||||
| ZS | ||||||||||||||||||
| 20 | 24 | 212 | 28 | |||||||||||||||
| 21 | 25 | 213 | 29 | |||||||||||||||
| 23 | 27 | 215 | 211 | |||||||||||||||
| 22 | 26 | 214 | 210 | |||||||||||||||
Теоретико-множественные и алгебраические операции при описании функции на логико-математическом уровне конкретизируются в наборе логических операций:
R Û {┐; Ù;Ú;┐Ú;¯;┐Ù; / ; ®;«; Å ... }.
Задачи и упражнения
1. Составьте алгебраические системы для следующих логических операций: отрицание(┐), дизъюнкция(Ú), конъюнкция(Ù), импликация(®), эквиваленция(º). Как называются подобные таблицы в математической логике?
2. Для одной из ячеек системы высказываний таблицы Жукова, определяющей краткий план работ в саду и огороде, постройте логические формулы, введя соответствующую систему обозначений для множества правильных высказываний.
Сколько ячеек может содержать таблица Жукова? Введите для таблицы Жукова понятие "алгебраическая структура и операция".
3. Номер логической функции задан десятичным числом k из множества {0,.....65531}. Задайтесь числом k. Определите соответствующую этому числу логическую функцию. Воспользуйтесь картой Карно.
4. Составьте таблицу отношений N ® N, N2 ® N при N = {0;1}
опр
и N2 Û N * N.
Покажите, что логическая интерпретация определяет множество булевых функций от одной или 2-х переменных соответственно.
5. Определите изоморфизм диаграмм Эйлера, Венна, кубического графа на примере одной из логических функций.
6. Полные наборы функций определяют изоморфные формы их описания. Покажите изоморфизм логических систем на примерах наборов функций Пирса - Вебба (стрелка Пирса) и функции Шеффера (штрих Шеффера).
7. Определите системное свойство следующих наборов логических функций: {константа 0, отрицание, конъюнкция, дизъюнкция}; {отрицание, конъюнкция}; {отрицание, дизъюнкция}; {стрелка Пирса}; {штрих Шеффера}.
8. Определите систему соответствий логических операций, производимых на уровне множеств (У2), и на уровне моделей математической логики (У4).
9. Известны 11 элементарных логических функций, определяемых логической формулой и кортежами свойств: (a1; a2; a3; a4; a5);
0(a2;a3);1(a1;a3);  (a1;a2;a5);(x1Lx2)(a3;a4);(x1Vx2)(a3;a4);
(a1;a2;a5);(x1Lx2)(a3;a4);(x1Vx2)(a3;a4);
(x1 ® x2)(a1;a3;a4;a5);(x1»x2)(a1;a3;a5);(x1 x2)(a2;a3;a4;a5);
(x1Å x2)(a2;a3; a5);(x1/x2) (все свойства);
(x1 ¯ x2) (все свойства).
Дайте лингвистическое определение понятий, записанных выше.
Составьте соответствующую описанию таблицу в виде алгебраической операции.
ГЛАВА 3. ТОПОЛОГИЯ И ТОПОЛОГИЧЕСКИЕ
УРОВНИ ОПИСАНИЯ ОБЪЕКТА – У5
Всеобщие формы существования материи определяются понятиями пространства и времени.
Основные свойства материи являются общесистемными: материя несотворима, неуничтожима, вечна и бесконечна.
На уровне описания объекта системой высказываний, правильность которых проверяется историческим опытом людей, материя наделяется следующими свойствами:
1. Это философская категория для обозначения объективной реальности.
2. Основа (субстрат) всех реально существующих в мире свойств, связей и форм движения (всех процессов и явлений).
3. Бесконечное множество всех объектов и систем.
4. Субстанция (сущность), нечто относительно устойчивое, существующее само по себе, не зависит ни от чего другого.
Итак, объект является частью материального мира, выделенного субъектом для наблюдений. Объект участвует в общем движении, расположен в пространстве и проявляет себя во времени.
Движение характерно для объекта и как изменение его внутреннего состояния в пространстве параметров, так и относительно других объектов в метрических пространствах.
На топологических уровнях описания пространство рассматривается в свою очередь как система, наделенная определенными математическими свойствами. Вводятся пространственно-подобные отношения: метрика объекта, расстояние между объектами и между состояниями объекта, системы координат, нормированные пространства.
Объектами математических пространств являются точки, линии, плоскости, поверхности, вектора, числа и их комплексы.
Итак, описание системы на топологическом уровне конкретизируется по отношениям меры, т.е. вводятся пространственно-подобные отношения.
Дата добавления: 2015-07-30; просмотров: 1451;
