ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА

Пусть М - множество, V_m - система подмножеств множества М.

Система V_m называется топологией в М и имеет следующие свойства:

1. М Î V_m; I Î V_m; 2. " (G_i Ç G_k) Î V_m; 3. " (È G_i ) Î V_m.

Пример

Рассмотрим топологию базовых множеств: М = {Г;П;В}: Г - группа; П – пространство; В - время.

Топология для базирования объектов определяется множеством суммой множеств М.

Множества, принадлежащие системе V_m, называются открытыми множествами пространства (М; V_m).

Одно и то же М может порождать ряд топологий, а следовательно, и топологических пространств:

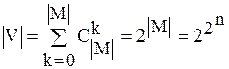V = Æ - отсутствие топологии.

Тривиальная топология - пространство слипшихся точек.

Дискретная топология, если открыто любое подмножество М.

Дата добавления: 2015-07-30; просмотров: 636;