СВОЙСТВА МЕРЫ НЕЧЕТКОСТИ
Мера нечеткости была предложена как функция для решения общей задачи
H: P ® [0, ¥] ,
где H - шенноновская энтропия,
P – множество всех распределений вероятностей, которые могут быть определены на конечных множествах альтернативных (взаимно-исключающих) выходах:
P = 0 для детерминированного случая;
иначе P ® ¥; подобно множеству точек отрезка [0,1], любая из которых может быть принята за разделительную для выделения отрезка Pi.
P1 P2 Pi Pn

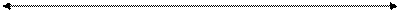
[0;1]
Сравнение по нечеткости множеств альтернатив разбиения универсума [0,1] на части целого {[Pi]} определяется в общем виде функцией H:
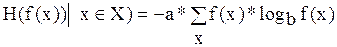 .
.
Это единственная известная функция, удовлетворяющая системе из пяти аксиом:
К(a) = (a1;a2;a3;a4;a5)H,
где
a1H - симметричность: нечеткость инвариантна относительно перестановки вероятностей;
a2H - расширяемость: нечеткость не меняется при добавлении к рассматриваемому множеству выходов с нулевой вероятностью;
a3H - квазиаддитивность: нечеткость совместного распределения вероятностей не более суммы нечеткостей соответствующих безусловных распределений его компонентов;
a4H - аддитивность: для распределения вероятностей любых 2-х независимых множеств выходов нечеткость совместного распределения вероятностей равна сумме нечеткостей отдельных распределений вероятностей;
a5H - непрерывность: нечеткость это непрерывная функция на всех своих аргументах.
Функция f(х) определяет нечеткость (в частности, вероятность) для конечного множества альтернатив х Î X.
Коэффициенты "a" и "b" в H являются конституэнтами: значение "а" используется на практике в качестве нормирующего коэффициента , значение "b" (основание логарифма) определяет единицу измерения при передаче информации (бит... дит...).
Нормализующее свойство меры нечеткости иллюстрируется нечеткостью 2-х равновероятных исходов, когда H = 1.
Чтобы нормализовать для произвольного множества исходов при наихудшем равновероятном случае альтернатив значение H нормируют по величине
| ld | X | | , где | X | - мощность (число) альтернатив;
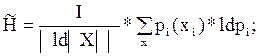
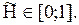
Значения нормы сведены в таблицу.
| | X | | ||||||||||
| ld | X | | 1.58 | 2.32 | 2.58 | 2.8 | 3.16 | 3.32 |
Упражнения
1. Система имеет два взаимоисключающих выхода на множестве альтернатив {0;1}. Определить норму.
2. Повторить для X = {3,4,5}.
3. Определить энтропию и нормализовать ее для следующих механизмов случайного выбора (МСВ).
а.
| МСВ | X1 | X2 |
| МСВ-R1 | 0.1 | 0.9 |
| МСВ-R2 | 0.3 | 0.7 |
| МСВ-R3 | 0.5 | 0.5 |
б.
| X | |||||
| Pl1 | 0.6 | 0.3 | 0.09 | 0.01 | - |
| Pl2 | 0.37 | 0.37 | 0.19 | 0.06 | 0.01 |
в.
| T | |||||||
| Pm | 0.01 | 0.06 | 0.24 | 0.38 | 0.24 | 0.06 | 0.01 |
4. В приложении 5 приведены вероятности появления букв в русском языке, а также один из возможных вариантов МСВ для имитационного моделирования процесса появления букв. “Переведите” на русский язык фрагмент таблицы случайных чисел (см. П.4), предварительно группируя числа в виде четырехзначных последовательностей.
5. Определите нечеткость преобразования последовательности символов “Основы теории систем “, используя данные приложения 6.
6. В приложении 6 приведена топология пишущей машинки с разметкой по частоте отдельных символов (см.П5).
а. Определите систему двухбуквенных сочетаний, используя отношение соседства на клавиатуре.
б. Оцените соответствие найденных соседств фонетическому строю русских слов. Приведите конкретные примеры в подтверждение типовых буквосочетаний и оцените удобство их печатания в данной топологии расположения символов: при печатании одним пальцем и при многопальцевой системе.
7. В приложении 7 приведена топология клавиатуры персонального компьютера (ПК). Определите системы соответствий между топологиями пишущей машинки и ПК. Какое лингвистическое и программно-математическое обеспечение потребуется для решения подобной задачи?
5. ДИНАМИЧЕСКИЙ УРОВЕНЬ ОПИСАНИЯ СИСТЕМ У7
Время и пространство неразрывны, как единая форма бытия.
Время - это форма последовательности смены явлений и состояний материи, оно характеризует длительности их бытия. Время - это измерение длительности процессов. Своеобразная топологическая мера со свойством однонаправленности. С понятием времени связаны понятия прошлое, настоящее, будущее, связана динамика процессов гибели и восстановления, адаптации, эволюции и т.д.
По свойствам время и пространство имеют общие черты: неотделимость от материи, неразрывность от движения, количественная и качественная бесконечность.
Универсальные свойства времени: длительность, неповторяемость, необратимость.
Системы измерения времени базируются на системах отсчета: суточное, годовое, звездное, солнечное, местное, всемирное (по Гринвичу), поясное (декретное), эфемеридное.
Эфемеридное время - равномерно текущее время: эфемеридная секунда равна (31.556.925,9747)-1 доля тропического года по данным за 1900 год, январь 0, в 12 часов.
В науке на теоретико-множественном уровне абстрагирования время определяется как однонаправленное множество T с элементами tÎT, с дискретно-задаваемым или непрерывным отсчетом по шкале чисел N. Точки начала и конца отсчета времени определяются наблюдателем.
Системы, описание которых базируется на множестве Т, определяются как динамические системы, в отличие от статических, т.е. не меняющих свои состояния в зависимости от времени.
Дата добавления: 2015-07-30; просмотров: 967;
