Построение логарифмических частотных характеристик (ЛАХ).

Передаточная функция (6.3) представляется набором типовых звеньев (интегрирующего, двух инерционных и форсирующего)

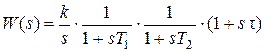. (2.106)

На одном графике в масштабе изображаются графики логарифмических частотных характеристик типовых звеньев. Полученные кривые графически суммируются, образуя ЛАХ системы в разомкнутом состоянии (графики L(ω) и ϕ(ω) точно один под другим) (см. рис. 2.36).

Рис. 2.36. ЛАХ рассматриваемого примера

Показатели качества, определенные по этим характеристикам:

ω_ср = 1000 1/c, ω_кр = 2,300 1/с, ∆L(ω) = 14 дБ, ∆ϕ(ω) = 20°. (2.107)

Запретная зона по точности, изображенная на рис. 2.36, для рассматриваемой системы первого порядка астатизма представлена на рис. 2.33 b. Параметры контрольной точки рассчитываются в соответствии с требованиями по точности (6.4).

.

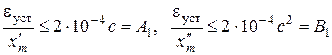ω_x = A₁/B₁ = 1, L(ω_x) = 20lg(B₁/ 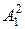) = 74 дБ.

Запретной зоны по колебательности. Допустимое значение показателя колебательности M_д = 1,5. Вычисляются значения уровней контрольных линий (см. раздел 5.2):

20lg( 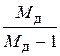) = 20lg( 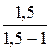) = 9,5 дБ,

20lg( 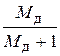) = 20lg( 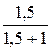) = – 4,4 дБ

и по графику логарифмической амплитудно – частотной характеристики L = L(w) определяются значения частот ω_a и ω_b, позволяющих определить положение точек A и B на фазовой характеристике. Знание значения угла ∆γ = arcsin(1/M_д) = arcsin(1/1,5) = 41,8° позволяет построить дугу ACB, определяющую запретную зону.

Анализ полученных результатов позволяет сделать следующие заключения:

· ω_ср < ω_кр, следовательно, исходная система устойчива.

· Запас устойчивости по амплитуде ∆L(ω) достаточный, а по фазе ∆ϕ(ω) – меньше указанного в техническом задании.

· Наклон логарифмической амплитудно–частотной характеристики ∆L(ω) в районе частоты среза ω_ср равен –40 дБ/дек, что указывает на колебательный характер переходной характеристики и, следовательно, недостаточный запас устойчивости системы.

· Логарифмическая амплитудно – частотная характеристика пересекает запретную зону по точности. Это свидетельствует о невыполнении технического условия точности по скорости регулярного входного воздействия (см. рис. 14).

2.10.2.2. Построение амплитудно – фазовой характеристики (АФХ).

В большинстве случаев информации, полученной на основе анализа ЛАХ, бывает достаточной. Но иногда необходимо привлечение еще и данных, полученных в результате исследования амплитудно – частотной характеристики (АФХ) системы в разомкнутом состоянии. В рассматриваемом примере вызывает сомнение определение значения критической частоты ω_кр, признанного ранее равным 2,300 1/с. Но фазовая характеристика ϕ(ω) достигает уровня –180° еще и при 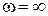. Разрешить эту проблему можно только с помощью АФХ.

Для построения приближенной характеристики АФХ, используются построенные ранее графики логарифмических частотных характеристик (рис.2.37). При этом для определения полярных координат комплексного коэффициента передачи K(jω) удобно заполнить таблицу (см. табл. 5).

Таблица 5 Таблица 6

A(ω)	L(ω) дБ	ω 1/с	ϕ(ω) гр.
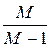
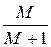
			–160		3,0	1,5	0,75
			–150		2,5	1,6	0,71
			–140		2,0	2,0	0,67
0,5	–6		–175		1,5	3,0	0,60
0,2	–14		–180		1,2	6,0	0,55

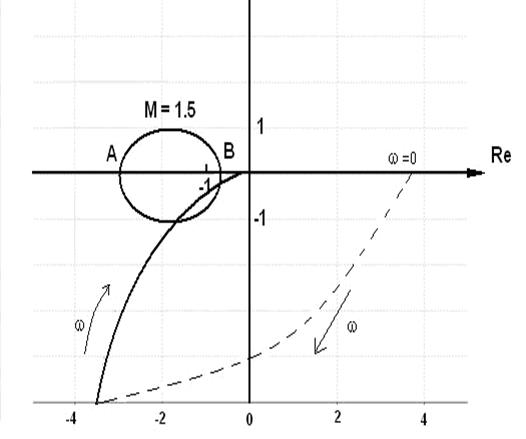
Рис. 2.37. АФХ рассматриваемого примера

Задавая значения амплитуды A(ω), вычисляется величина L(ω) = 20lg(A(ω)). На графике рис.2.37 проводится горизонтальная прямая до пересечения с ломаной L = L(ω). Из полученной точки проводится вертикаль, позволяющая определить значения ω и ϕ(ω). Координаты A(ω) и ϕ(ω) определяют точку на комплексной плоскости амплитудно – фазовой характеристики. Около нее подписывается найденное ранее значение частоты ω. Характеристика дополняется дугой бесконечного радиуса, поворачивающую видимую её часть против часовой стрелки на угол, равный 90° (поскольку передаточная функция W(s) содержит одно интегрирующее звено

На график АФХ наносятся линии постоянного уровня показателя колебательности M. В таблице 6 представлены значения показателя M и значения постоянных 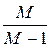, , 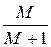позволяющих определить координаты точек A(– 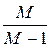,0) и B(– 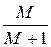,0) – концов диаметров окружностей указанных линии постоянного уровня. Область внутри окружности уровня M = 1,5 является запретной зоной по колебательности. График АФХ пересекает эту зону, следовательно, показатель колебательности рассматриваемой системы больше чем 1,5. Действительно, окружность уровня M = 2,5 касается графика АФХ в точке, когда ω = ω_m , т.е. M = 2,5. Частота ω_m близка к частоте среза ω_ср.

Анализ полученных результатов позволяет сделать следующие заключения:

· АФХ системы в разомкнутом состоянии не охватывает точку (–1,0), следовательно, исходная система (в замкнутом состоянии) устойчива.

· Из положения, приведенного в предыдущем пункте, вытекает неравенство ω_ср < ω_кр и это еще один признак того, что исходная система устойчива.

· График АФХ пересекает запретную зону по колебательности. Действительно, показатель колебательности равен 2,5,т.е. M > M_д.