Случайные ошибки в установившемся режиме
Влияние случайной составляющей ошибки на работу системы характеризуются дисперсией ошибки σe (4.13) и величиной шумовой полосы ∆Fэ (4.18). Для вычисления этих параметров требуется вычислить интеграл (4.16). В соответствии с выражениями (4.6) и (4.11) комплексный коэффициент передачи случайной ошибки в обозначениях формул (6.9) равен
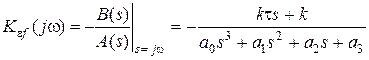 . (2.113)
. (2.113)
В обозначениях интеграла (6.12)
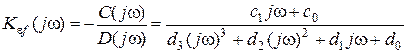 .
.
Таким образом, с учетом (4.15) имеем
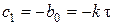 = – 2,
= – 2, 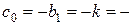 2000.
2000.
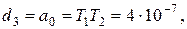
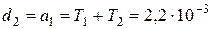 ,
, 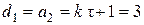 ,
,
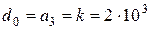 .
.
Подставляя полученные значения в формулу (6.12) вычисляется интеграл J3 и в соответствии с формулами (4.17) и (4.18) – значения параметров se2, ∆Fэ.
J3 = 724, ∆Fэ = 362 Гц, se2 = 724 Sf(0).
 2.10.2. Применение последовательного корректирующего фильтра
2.10.2. Применение последовательного корректирующего фильтра
Итак, исходная система устойчива, но не удовлетворяет требованиям технического задания по точности и запасам устойчивости. Как отмечалось в разделе 6.1 для удовлетворения требованиям точности необходимо увеличить коэффициент усиления k так, чтобы логарифмическая амплитудно – частотная характеристика проходила выше запретной зоны по точности.
 , (2.114)
, (2.114)
где
kрез – коэффициент усиления результирующей системы,
kис – коэффициент усиления исходной системы,
kкор – коэффициент усиления корректирующего фильтра.
Для рассматриваемого примера минимальное значение коэффициента усиления равно kкор = 2 (в этом случае ломаная L = L(ω) «лежит» на границе запретной зоны).
Ниже будут рассмотрены два варианта коррекции исходной системы
1. На рис. 16 представлены графики ЛАХ дляварианта с применением фильтра с опережением по фазе с параметрами
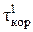 = 0,002 c,
= 0,002 c,  = 0,0001 c.
= 0,0001 c.
На рис. 2.38 изображены графики ЛАХ для варианта с применением фильтра с запаздыванием по фазе с параметрами
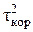 = 0,02 c,
= 0,02 c, 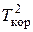 = 0,5 c.
= 0,5 c.
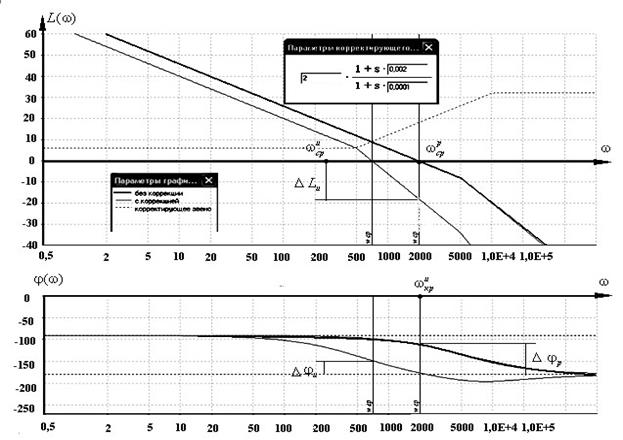
Рис. 2.38. Вариант 1 применения фильтра с опережением по фазе
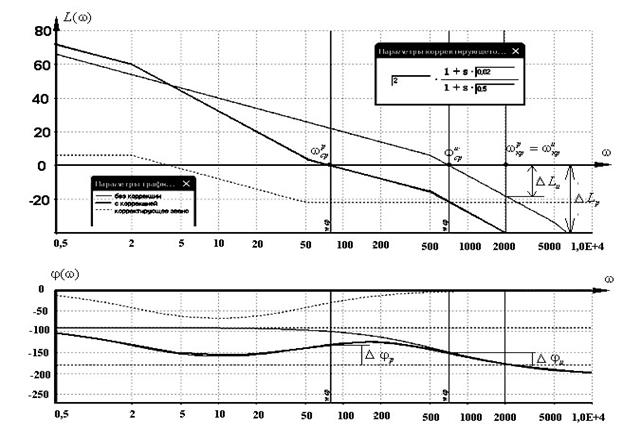
Рис. 2.39. Вариант 2 применения фильтра с запаздыванием по фазе.
Графики ЛАХ подобные тем, что изображены на рис.2.38 и рис. 2.39, входят в состав индивидуального домашнего задания, выполняемого студентом до соответствующей лабораторной работы. В процессе выполнения указанной лабораторной работы с применением программных продуктов PTSystem и PTSystem_New появляется возможность на экране дисплея иметь графики АФХ, 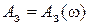 и переходной характеристики, рассчитанные значения показателей точности системы. Это позволяет уточнить предложенные варианты и выбрать из них наилучшие с той или иной точки зрения. Графики переходных характеристик и АЧХ системы в замкнутом состоянии для рассматриваемых вариантов результирующих систем представлены на рис. 2.40 – рис.2.43.
и переходной характеристики, рассчитанные значения показателей точности системы. Это позволяет уточнить предложенные варианты и выбрать из них наилучшие с той или иной точки зрения. Графики переходных характеристик и АЧХ системы в замкнутом состоянии для рассматриваемых вариантов результирующих систем представлены на рис. 2.40 – рис.2.43.
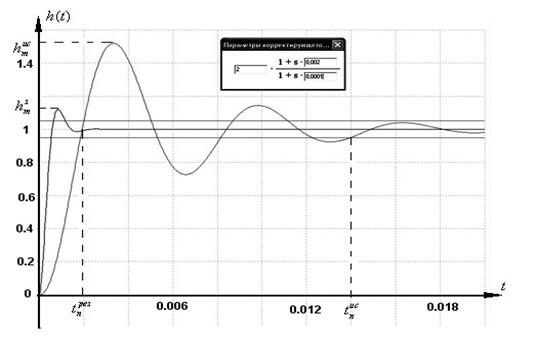
Рис. 2.40. Вариант 1. Переходная характеристика.
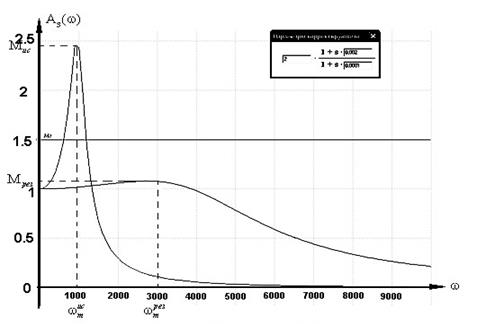
Рис. 2.41. Вариант 1. АЧХ
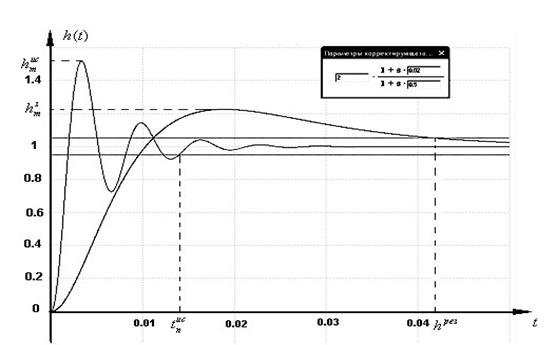
Рис. 2.42. Вариант 2. Переходная характеристика
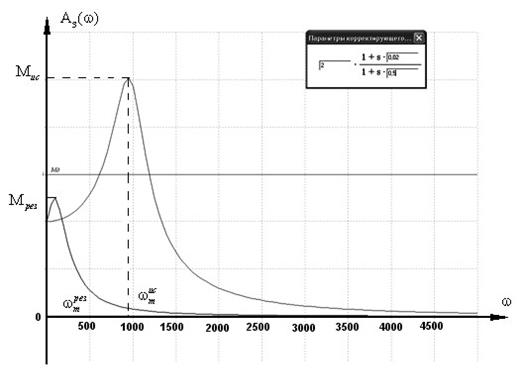
Рис. 2.43. Вариант 2. АЧХ
В таблице 7 приведены значения показателей качества исходной и двух вариантов результирующих систем. Параметры ωср, ωкр, ∆L, ∆ϕ, M получены на основе анализа частотных характеристик. Показатели точности γ1, γ2, ∆F – рассчитаны по формулам, перерегулирование σ и время переходного процесса tп получены с использованием программного обеспечения, разработанного на кафедре. Для сравнения в первой строке рассматриваемой таблицы приведены данные технического задания.
Таблица 7
| ωср 1/c | ωкр 1/c | ∆LдБ | ∆ϕ гр. | M | 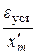 с
(γ1) с
(γ1)
| 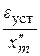 с2
(γ2) с2
(γ2)
| ∆F Гц | σ% | tп с | |
| Техническ. Задание | ³14 | ³30° | £1,5 | £2 10-4 | £2 10-4 | £30% | ||||
| Исходная система | 20° | 2,5 | 5 10-4 | 3,5 10-7 | 52,7% | 1,4 10-3 | ||||
| Система варианта 1 |
|
| 45° | 1,1 | 2,5 10-4 | –1,2 10-8 | 11,6% | 1,3 10-2 | ||
| Система варианта 2 | 50° | 1,25 | 2,5 10-4 | 1,2 10-8 | 22,6% | 4,2 10-2 |
Дата добавления: 2015-07-30; просмотров: 1025;
