Теорема Гаусса в дифференциальной форме
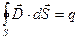
Теорема Гаусса в интегральной форме
С помощью теоремы Гаусса в интегральной форме нельзя определить, как связан исток линий 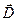 вектора электрического смещения в данной точке поля с плотностью свободных зарядов в этой же точке. Чтобы узнать это, рассмотрим дифференциальную форму теоремы Гаусса. Для этого разделим обе части уравнения интегральной формы записи теоремы Гаусса на одну и туже скалярную величину V (объем), находящийся внутри замкнутой поверхности:
вектора электрического смещения в данной точке поля с плотностью свободных зарядов в этой же точке. Чтобы узнать это, рассмотрим дифференциальную форму теоремы Гаусса. Для этого разделим обе части уравнения интегральной формы записи теоремы Гаусса на одну и туже скалярную величину V (объем), находящийся внутри замкнутой поверхности:
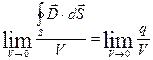 .
.
Это выражение справедливо для V любой величины, устремим V к 0.
Предел отношения потока вектора электрического смещения сквозь замкнутую поверхность, ограничивающую некоторый объем, к объему называют дивергенцией вектора 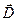 электрического смещения.
электрического смещения.
Или вместо слова «дивергенция» употребляют термины «расхождение».
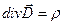 ,
,
где 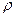 – объемная плотность заряда:
– объемная плотность заряда:
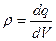 .
.
1. Если объемная плотность зарядов 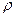 >0 в данной точке поля положительна, то из бесконечно малого объема окружающего данную точку поля, линии вектора электрического смещения исходят (исток).
>0 в данной точке поля положительна, то из бесконечно малого объема окружающего данную точку поля, линии вектора электрического смещения исходят (исток).
2. Если объемная плотность зарядов 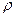 <0 в данной точке поля отрицательна, то в бесконечно малый объем окружающий данную точку поля, линии вектора электрического смещения входят (сток).
<0 в данной точке поля отрицательна, то в бесконечно малый объем окружающий данную точку поля, линии вектора электрического смещения входят (сток).
3. Если объемная плотность зарядов 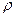 =0 в данной точке поля равна нулю, то в данной точке поля нет ни стока, ни истока. Линии вектора электрического смещения
=0 в данной точке поля равна нулю, то в данной точке поля нет ни стока, ни истока. Линии вектора электрического смещения 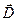 проходят через данную точку пространства.
проходят через данную точку пространства.
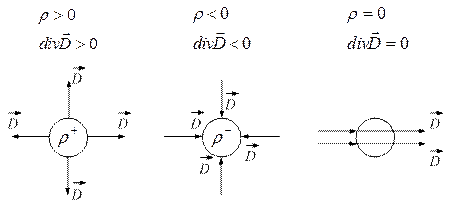
Силовые линии начинаются и заканчиваются на зарядах.
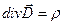
Теорема Гаусса в дифференциальной форме
Если среда однородна и изотропна, то ее 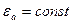 и тогда:
и тогда:
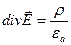 .
.
Разложим дивергенцию в декартовой системе координат:
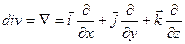 ;
;
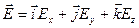 ;
;
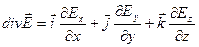 .
.
Мкость
Если два проводящих тела разделены диэлектриком и несут на себе равные по значению и противоположные по знаку заряды, то в пространстве между ними создается электрическое поле.
Под емкостью С между двумя телами, на которых имеются равные и противоположные по знаку заряды, понимают абсолютную величину отношения заряда на одном из тел к разности потенциалов между телами.
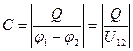 .
.
Емкость измеряется в Фарадах 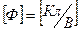 .
.
Емкостью обладают любые два тела, разделенные диэлектриком.
Техническое устройство определенной емкости – это конденсатор.
Емкость линейного конденсатора не зависит от заряда и разности потенциалов, а зависит от геометрических размеров конденсатора и свойств диэлектрика находящегося между пластинами.
Методика расчёта ёмкости тела правильной формы:
Условно считают заряд известным, через него выражают напряжение и подставляют в формулу для емкости, где заряд сокращают.
Емкость плоского конденсатора
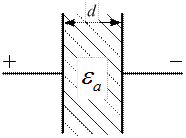
Применим теорему Гаусса в интегральной форме:
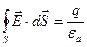 .
.
Поле плоского конденсатора равномерно, поэтому можно убрать знак интеграла:
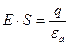 .
.
Заряд равномерно распределен по поверхности пластин, поэтому в расчетах удобно пользоваться понятием поверхностной плотности заряда.
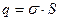 ;
;
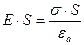 ;
;
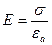 .
.
Зная напряженность электростатического поля 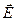 найдем напряжение:
найдем напряжение:
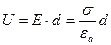 .
.
Тогда
 .
.
Ёмкость цилиндрического конденсатора
(коаксиального кабеля)

Напряженность поля цилиндрического конденсатора (см. применение теоремы Гаусса):
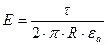 .
.
Зная напряженность электростатического поля 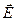 найдем напряжение:
найдем напряжение:
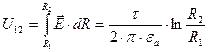 .
.
Заряд распределен по длине.
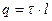 ,
,
где l – длина кабеля.
Тогда емкость цилиндрического конденсатора:
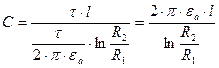 .
.
Ёмкость двух проводной линии

Если d >> Rn , то 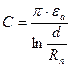 .
.
Если d ≈ Rn , то 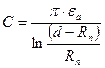 .
.
Ёмкость сферического конденсатора
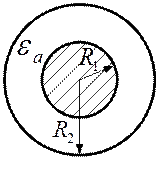
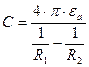 .
.
Если R2 устремить к бесконечности, то получим формулу для шара:
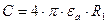 .
.
Ёмкость двухслойного цилиндрического конденсатора
Поверхность каждого слоя эквипотенциальна, поэтому её можно заменить металлической поверхностью, сообщив некоторый потенциал 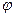 (второе следствие теоремы единственности решения). Получим два конденсатора один внутри другого.
(второе следствие теоремы единственности решения). Получим два конденсатора один внутри другого.

+
Конденсаторы соединим последовательно:
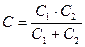 ;
;
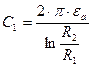 ;
; 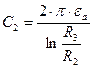 ;
;
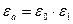 ;
; 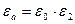 .
.
Дата добавления: 2015-07-30; просмотров: 2162;
