Граничные условия
В электростатическом поле рассматривают два типа границ:
1. Диэлектрик – Проводник.
2. Диэлектрик – Диэлектрик.
Для каждого типа границы есть два граничных условия:
1. Для первого типа границы Диэлектрик – Проводник:
а) отсутствует тангенциальная (касательная к поверхности) составляющая вектора напряженности электрического поля
 .
.
б) вектор электрического смещения D в любой точке диэлектрика, непосредственно примыкающей к поверхности тела, численно равен плотности заряда на поверхности проводящего тела в этой точке
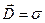
Докажем это:
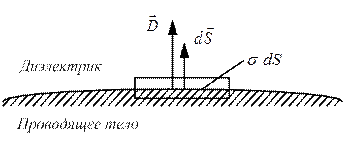
а) Так как тело проводящее 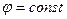 , то
, то 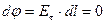 .
.
Так как 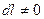 , то
, то 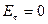 .
.
б) Мысленно выделим бесконечно малый параллелепипед. Верхняя грань расположена на поверхности проводящего тела, нижняя в диэлектрике. Параллелепипед малой толщины (сплющенный). Применим к нему теорему Гаусса в интегральной форме
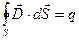 .
.
Пренебрегаем потоком через боковые грани, так как параллелепипед плоский. Поток через «дно» отсутствует, так внутри проводящего тела  и
и 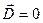 . Есть поток только через верхнею грань
. Есть поток только через верхнею грань 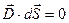 .
.
Тогда теорема Гаусса запишется:
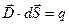 .
.
Так как угол между вектором 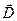 и вектором нормали
и вектором нормали 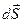 равен нулю, то:
равен нулю, то:
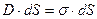 ;
;
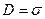 .
.
2. Для второго типа границы Диэлектрик – Диэлектрик:
а) тангенциальные составляющие поля равны
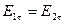 .
.
б) равны нормальные составляющие электрического смещения
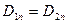 .
.

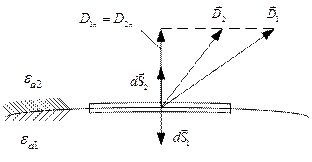
Докажем это:
а) Выделим плоский замкнутый контур mnpqm и составим вдоль него циркуляцию вектора напряженности электрического поля. Составляющими интеграла 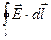 вдоль вертикальных сторон в силу их малости пренебрежем.
вдоль вертикальных сторон в силу их малости пренебрежем.
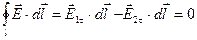 ;
;
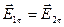 .
.
б) Мысленно выделим на границе раздела двух сред бесконечно малый параллелепипед. Внутри выделенного объема нет свободных зарядов, поэтому
 .
.
Поток вектора 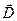 через верхнею грань:
через верхнею грань:
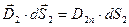 .
.
Поток вектора 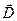 через нижнюю грань:
через нижнюю грань:
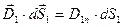 ;
;
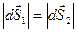 ;
;
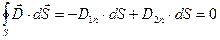 ;
;
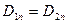 .
.
Если вектор электрического смещения 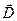 подходит под 90 градусов к границе раздела, то
подходит под 90 градусов к границе раздела, то 

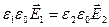 ;
;
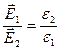 .
.
Граничные условия необходимо учитывать для любой задачи расчета поля вблизи 2–х сред. На их базе разработан ряд методов для расчета полей в пограничной зоне.
Дата добавления: 2015-07-30; просмотров: 4303;
