Основы теории систем массового обслуживания

При многономенклатурном производстве в функционирование производственной системы привносится элемент случайности, поскольку возможно появление внеочередного заказа или перечень заказов заранее неизвестен и последовательность работы определяется их поступлением в процессе функционирования системы. Кроме того, на ритмичность работы системы влияют такие факторы как дефицит ресурсов, отказы технологического оборудования и др. Производственный процесс в таких условиях приобретает признаки случайного процесса и этот элемент случайности необходимо учитывать при управлении автоматизированным производством.

Для моделирования функционирования производственной системы в рассматриваемом случае находит применение теория систем массового обслуживания. Производственная система должна изготавливать изделия в соответствии с потоком заказов-заявок. Система состоит из конечного числа единиц оборудования – каналов обслуживания. Обслуживание каждой заявки продолжается некоторое время, после чего канал обслуживания освобождается и снова готов для обслуживания следующей заявки. Заявки поступают одна за другой в некоторые, вообще говоря, случайные моменты времени.

При оценке работы производственной системы необходимо установить зависимость между характером потока заявок, производительностью отдельного канала, числом каналов обслуживания и эффективностью выполнения производственных заказов (заявок).

В качестве характеристик эффективности используются: среднее время простоя каналов обслуживания и производственной системы в целом; среднее время ожидания заявки в очереди; вероятность немедленного обслуживания поступившей заявки, средний процент отклоненных заявок и др. Каждая из этих характеристик даёт представление о пропускной способности (производительности) производственной системы.

Если рассматривать производственную систему как систему массового обслуживания, то процесс её функционирования будет случайным процессом. Этот процесс характеризуется сменой дискретных состояний системы в случайные моменты времени: изменение числа заявок в очереди, изменение числа занятых каналов и т.п. Смена дискретных состояний системы образует поток событий.

Важной характеристикой потока является закон распределения длины промежутка времени между сменой состояний. Часто при анализе систем массового обслуживания рассматривается простейший поток событий (стационарный пуассоновский поток), функция распределения которого соответствует экспоненциальному закону распределения

,

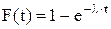где t – текущее время, l – параметр распределения.

Важной характеристикой системы массового обслуживания является время обслуживания одной заявки T_об. Эта величина может быть как случайной, так и неслучайной. Чаще всего время обслуживания случайно. Тогда характеристикой времени обслуживания будет функция распределения. Для описания этой функции часто используется закон экспоненциального распределения с плотностью вероятности

,

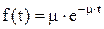где m – параметр распределения, величина обратная среднему времени обслуживания одной заявки.

При поступлении очередной заявки на обслуживание в систему массового обслуживания (очередной заказ для производственной системы), она становится в очередь и ждёт, пока система не освободится от обслуживания предыдущих заявок. Такие системы массового обслуживания называются системами с ожиданием. На ожидание могут накладываться ограничения: ограничение времени ожидания, ограничение длины очереди и др.

Пусть на вход системы массового обслуживания X с ожиданием, имеющей n каналов обслуживания, поступает простейший поток заявок с параметром l. Время обслуживания одной заявки T_об подчиняется экспоненциальному закону распределения с параметром

,

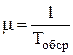где T_обср – среднее время обслуживания одной заявки.

Заявка, заставшая все каналы системы занятыми, становится в очередь и ожидает обслуживания. Время ожидания ограничено сроком T_ож. Если в течение этого времени заявка не будет обслужена, то она отменяется. Пусть T_ож величина случайная и распределена по экспоненциальному закону с параметром n.

В рассматриваемой системе возможны следующие состояния:

x₀ – система свободна, очереди нет;

x₁ – занят только один канал системы;

……

x_k – занято k каналов, очереди нет;

……

x_n – заняты все n каналов, очереди нет;

x_n+1 – заняты все n каналов, одна заявка в очереди;

……

x_n+s – заняты все n каналов, s заявок в очереди.

В принципе такая система может иметь бесконечное множество состояний. Каждое состояние характеризуется вероятностью, описываемой некоторым законом распределения. Плотность p_k вероятности k – того состояния при условии 0 £ k £ n можно описать уравнением Эрланга

.

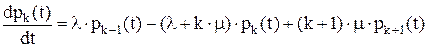Похожее дифференциальное уравнение можно составить для
k > n.

Таким образом, можно получить систему из бесконечного числа дифференциальных уравнений. Поскольку при больших значениях s вероятности становятся пренебрежимо малыми, то число уравнений при решении системы ограничивают. Решение системы уравнений позволяет получить выражения для оценки параметров системы.

Вероятности состояний системы массового обслуживания с ожиданием

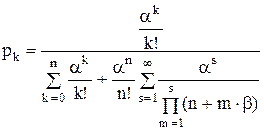при 0 £ k £ n,

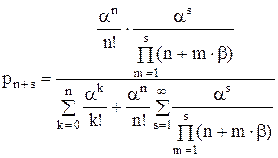при k > n (s ³ 1),

где 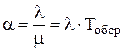, , 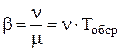T_обср – средняя длительность обслуживания заявки.

Использование этих формул позволяет, например, вычислить среднее число заявок в очереди

.

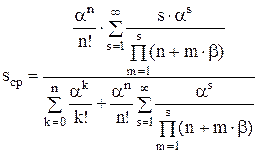Можно определить и другие параметры системы массового обслуживания: вероятность отклонения заявки, пропускная способность системы и др.

Рассмотрен анализ системы массового обслуживания с ожиданием. Существуют и другие типы систем массового обслуживания, для описания которых применяются свои математические модели, основанные на теории вероятности.