Основные определения и свойства сетей Петри
Эффективным инструментом моделирования дискретных процессов являются сети Петри – графы специального вида. Их основное достоинство – возможность отображать параллелизм, асинхронность, иерархичность объектов простыми средствами.
При моделировании дискретных процессов необходимо ответить на следующие вопросы: как взаимодействуют отдельные компоненты системы; имеются ли в системе потенциально "узкие" места; могут ли в системе возникнуть нарушения функционирования, сбои, и как можно их локализовать; можно ли упростить систему, заменив ее отдельные компоненты; может ли система выполнять те функции, для которых предназначена. То есть исследователя в первую очередь интересуют структурные характеристики и свойства проектируемого объекта.
Основой сети Петри является понятие условно-событийной системы. Компоненты системы, их состояния и действия представляются абстрактными понятиями, такими как условия и события. Событие может произойти (реализоваться) один раз, повториться многократно или не произойти ни разу. Для того чтобы событие произошло, необходимо появление ситуации, в которой это событие может быть реализовано. При этом ситуация определяется как совокупность некоторых условийвозникновения события. Иначе, событие совершается, если выполнены условия его реализации, определяемые в свою очередь состоянием системы. В результате совершения события происходит изменение условий и наступление постусловий реализации события.
Сеть Петри представляется как набор описаний следующего вида
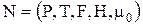 ,
,
где Р – конечное множество состояний pi (позиций); Т – конечное множество событий ti (переходов из состояния в состояние);  – функция входных инциденций (отношений связи), отображает связи между позициями и переходами;
– функция входных инциденций (отношений связи), отображает связи между позициями и переходами; 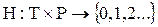 – функция выходных инциденций (отношений связи), отображает связи между переходами и позициями;
– функция выходных инциденций (отношений связи), отображает связи между переходами и позициями; 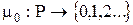 – начальная маркировка (разметка) сети, определяющая её состояние в начале функционирования.
– начальная маркировка (разметка) сети, определяющая её состояние в начале функционирования.
Графическим выражением сети Петри является ориентированный граф с двумя типами вершин: состояния и события. Дуги графов соответствуют связям состояний и событий. Состояние на графе изображается кружками, а события – вертикальными черточками (барьерами). Пример элементарной сети Петри приведен на рис. 238, а).
 Сеть имеет две позиции p1, p2 и один переход t1. Дуги (стрелки) графа отображают связь позиции p1 с переходом t1 и перехода t1 с позицией p2. Точка в позиции p1 использована для маркировки сети. Эта точка является маркером (фишкой) и означает, что сеть находится в состоянии, соответствующем позиции p1.
Сеть имеет две позиции p1, p2 и один переход t1. Дуги (стрелки) графа отображают связь позиции p1 с переходом t1 и перехода t1 с позицией p2. Точка в позиции p1 использована для маркировки сети. Эта точка является маркером (фишкой) и означает, что сеть находится в состоянии, соответствующем позиции p1.
Каждая дуга связывает вершины только разных типов: если дуга выходит из позиции, то должна войти в переход и наоборот. Позиции, из которых выходят дуги, направленные к данному переходу, называются его входными позициями. Позиции, в которые входят дуги, исходящие из данного перехода, называются его выходными позициями.
Смена состояний сети Петри (функционирование сети Петри) происходит при свершении (срабатывании) переходов. В элементарной сети при совершении перехода t1 произойдет смена позиций (состояний сети) p1 → p2. Переход является разрешённым (или возбуждённым) если выполнены условия для его совершения. Условием перехода t1 в элементарной сети, является нахождение сети в состоянии, соответствующем позиции p1.
Условие может иметь емкость: условие не выполнено (емкость равна нулю), условие выполнено (емкость равна единице), условие выполнено с n-кратным запасом (емкость равна n, где n – целое положительное число). На рис. 238, б показан случай, когда для выполнения перехода t1 необходимо выполнение условия нахождения в позиции p1 с двукратным запасом. Это обстоятельство отражено присутствием двух дуг, соединяющих вершину p1 с переходом t1.
Соответственно, свершение перехода может обеспечивать условие нахождения сети в определённой позиции с n-кратным запасом (рис. 238, в). Наличие условий для свершения переходов определяется наличием и числом маркеров в позициях сети. Наличие маркера в позиции p1 на рис. 238, а свидетельствует о том, что переход t1 разрешён, т.е. может произойти. Разрешённый переход происходит. Переход t1 в сети на рис. 238, б запрещён, т. к. для него условие p1 должно выполняться с двукратным запасом (в позиции p1 должны быть два маркера).
При свершении перехода из входной позиции забираются маркеры в количестве, соответствующем числу входных дуг, и передаются выходной позиции в количестве, определяемом числом выходных дуг (рис. 238, г). При этом состояние сети Петри и её маркировка изменяются.
В общем виде, когда переход связан со своими позициями кратными дугами, правило срабатывания перехода звучит так: при срабатывании перехода t1 он изымает из каждой своей входной позиции столько маркеров, какова кратность дуги, связывающей этот переход с указанной позиции, и добавляет в каждую свою выходную позицию количество маркеров, равное кратности связывающих их дуг.
В качестве примера опишем с использованием сети Петри работу станка. Для станка можно выделить следующие состояния: р1 – прибыла заготовка; р2 – станок свободен; р3 – станок работает; р4 – деталь обработана. Таким образом, припишем сети Петри множество состояний Р{р1,р2,р3,р4}. Для станка могут совершаться следующие события: 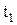 – началась обработка;
– началась обработка; 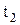 – закончилась обработка. Следовательно, сети Петри можно приписать множество переходов
– закончилась обработка. Следовательно, сети Петри можно приписать множество переходов 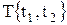 .
.
Вполне естественно, что конкретные состояния станочной системы могут допустить только вполне определенные события и наоборот – определенные состояния могут возникнуть только после определенных событий. Эта взаимосвязь определяется функциями инциденций. Для описываемого станка зависимость событий от состояний можно описать следующим образом (функция входных инциденций):
· начало обработки возможно только при наличии заготовки и свободном станке, или 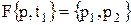 ;
;
· окончание обработки возможно только, если станок работал, или 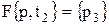 .
.
Аналогично опишем зависимость состояний от событий (функция выходных инциденций):
· состояние «станок работает» возможно, только после совершения события «началась обработка», или 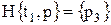 ;
;
· событие «закончилась обработка» влечет за собой переход в состояние «станок свободен» и «деталь обработана», или 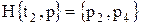 .
.
Отобразим описанные состояния и события вершинами ориентированного графа, а функции входных и выходных инциденций представим в виде ребер графа, соединяющих эти вершины (рис. 239, а). Полученный граф изображает сеть Петри, описывающую работу станка.
 Если ограничиться приведенными выше моментами, то по изображенному графу нельзя судить о состоянии сети Петри (и, следовательно, моделируемой станочной системы) в данный конкретный момент времени. Для отображения конкретного состояния сети Петри используется маркировка или разметка. Для разметки применяются маркеры, изображаемые точками.
Если ограничиться приведенными выше моментами, то по изображенному графу нельзя судить о состоянии сети Петри (и, следовательно, моделируемой станочной системы) в данный конкретный момент времени. Для отображения конкретного состояния сети Петри используется маркировка или разметка. Для разметки применяются маркеры, изображаемые точками.
Маркерами помечают состояния, в которых находится сеть Петри в данный момент (в кружках позиций ставятся точки).
Пусть рассматриваемая станочная система находится в исходном состоянии, которое характеризуется наличием, допустим, четырех заготовок и готовым к работе станком. Это состояние можно обозначить следующей начальной маркировкой сети Петри m0=(4,1,0,0). В скобках указаны значения возможных состояний последовательно для р1, р2, р3, р4. При этом нулем обозначается отсутствие данного состояния, а числом – его наличие с имеющимся n-кратным запасом (например, четыре заготовки). Начальная маркировка показана точками (рис. 239, а).
Одновременно в сети Петри возможны не все события, а только те, которые соответствуют наблюдаемому в данный момент времени набору состояний и, следовательно, разрешены. На графическом изображении сети Петри в данный момент времени разрешены те переходы, для которых все входные дуги связаны с маркированными состояниями (на рис. 239, а, разрешен переход 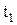 , поскольку для него входные ребра выходят из маркированных состояний р1 и р2).
, поскольку для него входные ребра выходят из маркированных состояний р1 и р2).
В процессе работы станка состояние станочной системы меняется (расходуются заготовки, появляются обработанные детали и т.д.). Это приводит к смене маркировок сети Петри (рис. 239, б). Последовательность смены маркировок или процесс функционирования сети Петри может быть отображен графом, вершинами которого являются возможные маркировки сети. Такой граф называется графом достижимости сети Петри. Для рассматриваемого примера граф достижимости линеен (рис. 240). В общем случае граф достижимости может иметь сложный разветвленный вид, если в сети Петри одновременно разрешены несколько переходов.
 При функционировании сети Петри возможна ситуация, когда ни один из переходов не разрешен. Это тупиковая ситуация (тупиковая маркировка), которую следует предотвращать для обеспечения работоспособности моделируемой станочной системы. Математическое выражение условия разрешенности перехода
При функционировании сети Петри возможна ситуация, когда ни один из переходов не разрешен. Это тупиковая ситуация (тупиковая маркировка), которую следует предотвращать для обеспечения работоспособности моделируемой станочной системы. Математическое выражение условия разрешенности перехода  имеет вид
имеет вид
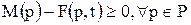 .
.
Это условие означает, что в каждой входной позиции перехода 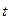 число маркеров должно быть не меньше веса дуги, соединяющей эту позицию (состояние) с переходом. Символ
число маркеров должно быть не меньше веса дуги, соединяющей эту позицию (состояние) с переходом. Символ 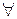 – квантор общности, значение которого «для всякого …». Выражение
– квантор общности, значение которого «для всякого …». Выражение 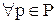 обозначает «для всякого р1, принадлежащего множеству Р».
обозначает «для всякого р1, принадлежащего множеству Р».
При срабатывании перехода (совершении события) возникает новая маркировка сети Петри
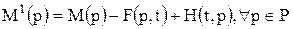 ,
,
т. е. в результате срабатывания из всех входных позиций перехода  изымается
изымается 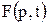 маркеров и в каждую входную позицию добавляется
маркеров и в каждую входную позицию добавляется 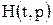 маркеров. В рассматриваемом примере после срабатывания перехода
маркеров. В рассматриваемом примере после срабатывания перехода 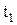 в первый раз новая маркировка сети Петри будет иметь вид (рис. 234, б).
в первый раз новая маркировка сети Петри будет иметь вид (рис. 234, б).
Пусть задана сеть Петри 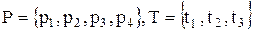 .
.
| t1 | t2 | t3 | p1 | p2 | p3 | p4 | ||||||
| p2 | t1 | |||||||||||
| F(p,t)= | p3 | H(t,p)= | t2 | |||||||||
| p4 | t3 | |||||||||||
| p5 |
 Изображение этой сети приведено на рис. 241. Оценим разрешенные переходы при начальной маркировке, используя функцию входных инциденций
Изображение этой сети приведено на рис. 241. Оценим разрешенные переходы при начальной маркировке, используя функцию входных инциденций
m0(р)=(1,1,1,1).
| p1 | p2 | p3 | p4 | ||
| t1 | Разрешен, | ||||
| t2 | Запрещен, | ||||
| t3 | Разрешен. |
Итак, из исходной маркировки разрешены переходы t1 и t3. Переход 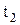 запрещен, поскольку для его осуществления недостаточно маркеров в позиции р2 (имеется только один маркер, а вес дуги графа, соединяющей р2 с
запрещен, поскольку для его осуществления недостаточно маркеров в позиции р2 (имеется только один маркер, а вес дуги графа, соединяющей р2 с 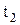 , равен двум).
, равен двум).
Множество всех маркировок, достижимых из начальной, называется множеством достижимости сети Петрии обозначается R(N).
Любая позиция или переход сети могут интерпретироваться как сеть Петри более низкого уровня. Это позволяет организовать многослойные иерархические сетевые структуры.
В сети Петри два возбужденных не взаимодействующих перехода могут сработать независимо друг от друга, поэтому моделям, использующим сети Петри, свойствен параллелизм или одновременность.
В зависимости от топологии сеть Петри называется:
1. Автономной сетью, если для каждого tÎТ имеется не более одной входной и не более одной выходной позиции, т.е. |·t|=| t·|=1.
2. Маркированным графом, если для каждого рÎРимеется только один входной и один выходной переходы, т. е. |·p|=| p·|=1.
3. Сетью свободного выбора, если для каждого tiÎТ и для каждого рiηtпозиция рi является либо единственной входной позицией перехода ti т.е. |рi|=1, либо этот переход имеет единственную входную позицию, т.е. |·ti|=1 (если два перехода имеют общую входную позицию, то эта позиция единственна для каждого из них).
Различают также простые сети, в которых любая пара переходов ti, tjÎT имеет не более одной общей входной позиции (т.е.|·ti  tj·|£1), и бесконфликтные сети, в которых для каждой позиции рÎР существует не более одной исходящей дуги |p·|£1 либо для всех tÎT выполняется условие tηp (т.е. любая позиция, являющаяся входной более чем для одного перехода, является также выходной для каждого такого перехода).
tj·|£1), и бесконфликтные сети, в которых для каждой позиции рÎР существует не более одной исходящей дуги |p·|£1 либо для всех tÎT выполняется условие tηp (т.е. любая позиция, являющаяся входной более чем для одного перехода, является также выходной для каждого такого перехода).
Таким образом, модель в виде сети Петри позволяет проследить развитие событий в реальной моделируемой системе и выявить тупиковые ситуации, которые необходимо избегать. Дальнейшее расширение возможностей применения сетей Петри достигается введением задержки маркера в данной позиции и введением разноцветных маркеров. Задержка маркера в позиции позволяет осуществить временное упорядочение событий моделируемого процесса и получить в результате моделирования привязку событий к конкретному времени, прошедшему с начала функционирования сети. При использовании задержки предполагается, что маркер не может покинуть позицию, в которую он прибыл, ранее, чем по истечении задержки, приписанной данной позиции. Так, после совершения события «началась обработка» в станочной системе и перемещение маркера в позицию р3 «станок работает» не может немедленно произойти событие «закончилась обработка», т. к. требуется определенное время qм на обработку. Этот факт может быть отражен задержкой маркера в позиции р3 на время qм. Следовательно, при определении разрешенных переходов учитывается соотношение времени задержки и времени протекания процесса.
Использование разноцветных маркеров позволяет проследить развитие событий в системе для маркеров с разным физическим смыслом. Так, для станочной системы, обрабатывающей детали разного типоразмера, можно каждому типоразмеру детали присвоить маркер своего цвета. Тогда сеть Петри позволит оценить особенности процесса для каждой детали отдельно.
Степень детализации сети Петри может быть различной. Так, в рассматриваемых выше примерах можно учесть большое число состояний, представить каждое событие в виде сети Петри и т.д. В этом смысле возможности сети Петри велики. Автоматизация моделирования систем с помощью сетей Петри достигается составлением алгоритмов и программ для расчета и анализа графа достижимости сети.
Дата добавления: 2015-07-30; просмотров: 3087;
